Понятие об устойчивости положения равновесия

Дополнительным воздействием на тело, находящееся в положении равновесия, сообщим ему небольшое отклонение.

Если после снятия этого воздействия тело возвращается в первоначальное положение, положение равновесия называется устойчивым в малом.

Если тело будет продолжать отклоняться - положение равновесия неустойчивое.

Если тело сохраняет отклоненное положение, то первоначальное положение равновесия безразличное.

Пример 10.1 (продолжение). Проанализируем устойчивость найденного положения равновесия (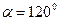) для стержня АВ, изображенного на рис. 10.2.

При отклонении стержня по часовой стрелке плечо силы 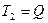увеличивается и, соответственно, увеличивается опрокидывающий момент. Одновременно уменьшаются плечи сил 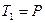и D, что вызывает уменьшение восстанавливающего момента. В таком случае стержень АВ продолжает свое отклонение.

При отклонении стержня против часовой стрелки плечо силы 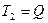уменьшается и, соответственно уменьшается ее момент, являющийся в этом случае восстанавливающим. Одновременно увеличиваются моменты сил 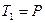и D и, будучи в данной ситуации опрокидывающими, вызывают дальнейшее отклонение стержня.

Таким образом, после небольшого отклонения в любую сторону, стержень АВ продолжает отклоняться, т.е. найденное положение равновесия неустойчиво.

Пример 10.2 (продолжение). Проанализируем устойчивость рабочего положения равновесия крана (см. рис.10.3). При значениях веса груза меньше максимально разрешенного (вычисленного в задаче), восстанавливающий момент больше момента опрокидывающего, т.е. заданное положение равновесия устойчиво.

При иных значениях веса груза кран продолжает отклоняться, т.е. равновесие крана неустойчиво.

Пример 10.3 (задача 9.25 из [ 2 ]). Найти предельную высоту H цилиндра, при которой тело, состоящее из цилиндра и половины шара одинаковой плотности и радиуса R, теряет устойчивость в положении равновесия, - когда оно опирается на гладкую горизонтальную плоскость.

На рис.10.4.а изображено тело, состоящее из половины шара и цилиндра, в прямом положении, а на рис. 10.4.б – в отклоненном. Точки 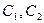и С – центры тяжести половины шара, цилиндра и составного тела; точка О – центр кривизны шаровой поверхности. Реакция гладкой поверхности N должна всегда проходить через точку О. Обе части тела обладают осевой симметрией; в силу этого центр тяжести С составного тела так же должен лежать на оси симметрии.

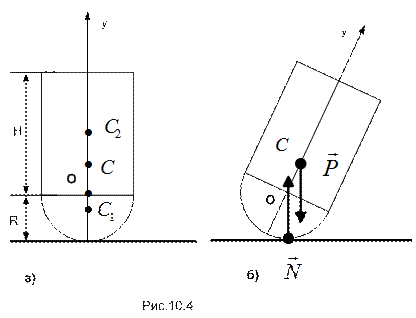
Анализ рисунков показывает, что если ордината центра тяжести тела располагается выше ординаты точки О, пара сил 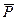и 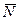создает опрокидывающий момент; в противном случае момент пары оказывается восстанавливающим (как у известной детской игрушки «Ванька – Встанька»). При совпадении точек С и О, тело находится в безразличном положении.

Учитывая однородность частей тела, вычислим ординату его центра тяжести, и приравняем ее к радиусу кривизны R шаровой поверхности:

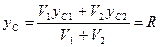
Где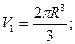

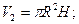
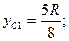
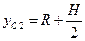
Отсюда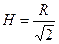

Примечание: особенностью рассмотренной задачи является перемещение точки приложения реакции опоры 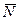в процессе наклона тела (она перемещается вдоль горизонтальной прямой; при этом сила нормального давления вертикальна и всегда проходит через точку О – центр кривизны шаровой поверхности).

Дата добавления: 2015-06-04