
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение. 1. Для определения реакции расчленим систему и рассмотрим сначала равновесие стержня DE (рис
|
|
|
|
1. Для определения реакции расчленим систему и рассмотрим сначала равновесие стержня DE (рис. С2, б). Проведем координатные оси xy и изобразим действующие на стержень силы: силу 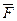 , реакцию
, реакцию 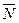 ,направленную перпендикулярно стержню, и составляющие
,направленную перпендикулярно стержню, и составляющие  реакции шарнира D. Для получения плоской системы сил составляем три уравнения равновесия:
реакции шарнира D. Для получения плоской системы сил составляем три уравнения равновесия:
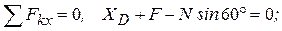 (1)
(1)
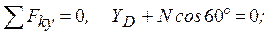 (2)
(2)
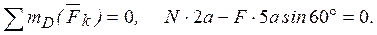 (3)
(3)
2. Теперь рассмотрим равновесие угольника (рис. С2, в). На него действуют сила давления стержня  , направленная противоположно реакции
, направленная противоположно реакции 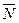 , равномерно распределенная нагрузка, которую заменяем силой
, равномерно распределенная нагрузка, которую заменяем силой 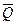 , приложенной в середине участка КВ (численно Q = q×4a = 16кН), пара сил с моментом М и реакция жесткой заделки, слагающаяся из силы, которую представим составляющими
, приложенной в середине участка КВ (численно Q = q×4a = 16кН), пара сил с моментом М и реакция жесткой заделки, слагающаяся из силы, которую представим составляющими 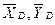 , и пары с моментом МА. Для этой плоской системы сил тоже составляем три уравнения равновесия:
, и пары с моментом МА. Для этой плоской системы сил тоже составляем три уравнения равновесия:
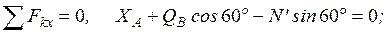 (4)
(4)
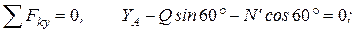 (5)
(5)
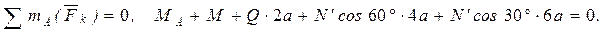 (6)
(6)
При вычислении момента силы разлагаем ее на составляющие 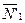 и
и 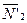 и применяем теорему Вариньона. Подставив, в составленные уравнения числовые значения заданных величин, и решив систему уравнений (1) – (6), найдем искомые реакции. При решении учитываем, что численно N’=N в силу равенства действия и противодействия.
и применяем теорему Вариньона. Подставив, в составленные уравнения числовые значения заданных величин, и решив систему уравнений (1) – (6), найдем искомые реакции. При решении учитываем, что численно N’=N в силу равенства действия и противодействия.
Здесь также необходимо выполнить проверку правильности определения реакций путем составления уравнения моментов относительно точки соединения составных частей конструкции (точки С) для всей системы в целом.
Ответ: N= 21,7 кН, YD=-10,8 кН; ХD=8,8 кН,ХА=-26,8кН, УА = 24,7 кН,
МА = -42,6кН×м. Знаки указывают, что силы 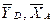 и момент МА направлены противоположно показанным на рисунках.
и момент МА направлены противоположно показанным на рисунках.
Задача С3
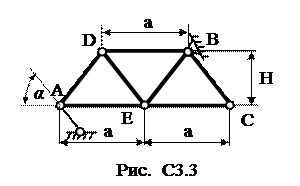
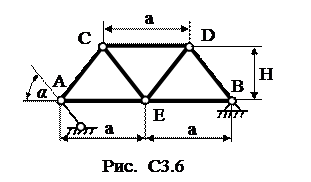
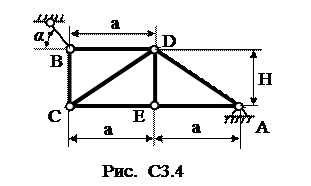
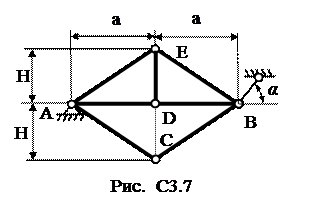
Ферма, состоящая из 7 стержней, и пяти узлов закреплена, как показано на рис. С3.0. - С3.9. В узлах фермы приложены две сосредоточенные силы, значения которых и точки их приложения указаны в таблице С3. Здесь же даны размеры фермы. Требуется методом вырезания узлов определить усилия во всех стержнях фермы. Для трех стержней фермы (по усмотрению студента) сделать проверку методом сечений. При расчете принять α=600.
Указание. Вначале необходимо составить уравнения равновесия для всей фермы в целом, и определить три неизвестные реакции опор.
Таблица С3
| Силы | 
| 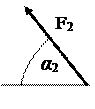
| 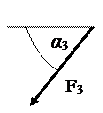
| 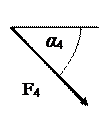
| ||||||
| F1= 10 кH | F2= 20 кH | F3= 30 кH | F4= 40 кH | |||||||
| Номер условия | а, м | H, м | Точка приложения | α1 град | Точка приложения | α2 град | Точка приложения | α3 град | Точка приложения | α4 град |
| С | - | - | - | - | D | |||||
| - | - | E | C | - | - | |||||
| E | - | - | - | - | C | |||||
| - | - | E | C | - | - | |||||
| C | - | - | - | - | D | |||||
| - | - | D | - | - | C | |||||
| E | - | - | C | - | - | |||||
| - | - | C | - | - | E | |||||
| E | - | - | D | - | - | |||||
| - | - | D | C | - | - |
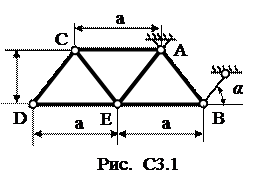
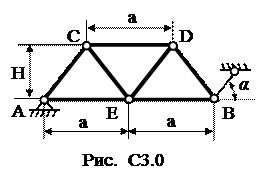


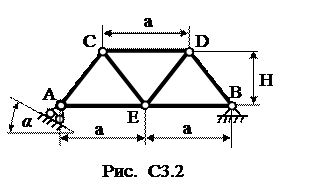
 |
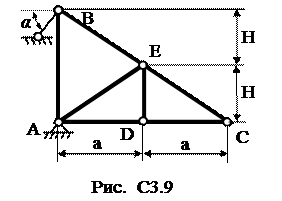

Пример С3.
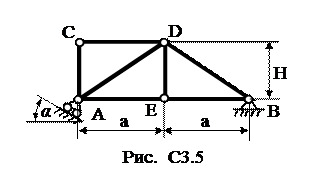
 В узлах фермы С и D (рис. С3) приложены силы: F1 =10 кH, и F2 =20 кH. Определить усилия во всех стержнях фермы методом вырезания узлов. Кроме того, определить усилия в стержнях 2, 3, 4 методом сечений. Размеры указаны на рисунке.
В узлах фермы С и D (рис. С3) приложены силы: F1 =10 кH, и F2 =20 кH. Определить усилия во всех стержнях фермы методом вырезания узлов. Кроме того, определить усилия в стержнях 2, 3, 4 методом сечений. Размеры указаны на рисунке.
1. Определим реакции опор: xA, yA, RB.
Для этого составим уравнения равновесия для всей фермы в целом.
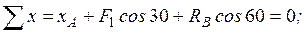 (1)
(1)
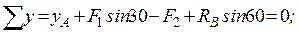 (2)
(2)
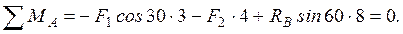 (3)
(3)
Решая уравнения (1,2,3), находим: xA = - 16,309 кН; yA = 1,752 кН; RB = 15,297 кН.
 2. Определим усилия в стержнях фермы методом вырезания узлов. Вначале будем полагать, что все стержни растянуты, тогда их реакции будут направлены во внутрь стержней. Покажем все силы, действующие на узел А (рис. С3а). Поскольку в узле А сходится только 2 стержня, то усилия в этих стержнях можно определить из уравнений равновесия:
2. Определим усилия в стержнях фермы методом вырезания узлов. Вначале будем полагать, что все стержни растянуты, тогда их реакции будут направлены во внутрь стержней. Покажем все силы, действующие на узел А (рис. С3а). Поскольку в узле А сходится только 2 стержня, то усилия в этих стержнях можно определить из уравнений равновесия:
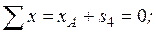 Отсюда:
Отсюда: 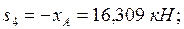
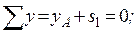
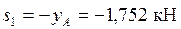
 Далее можно рассмотреть равновесие узла В (в нем сходится два стержня) или узла С (рис. С3б). В узле С сходится три стержня, но усилие s 1 нами уже определено, поэтому из уравнений равновесия можно найти s 2, s 3. Угол α определим из треугольника АЕС:
Далее можно рассмотреть равновесие узла В (в нем сходится два стержня) или узла С (рис. С3б). В узле С сходится три стержня, но усилие s 1 нами уже определено, поэтому из уравнений равновесия можно найти s 2, s 3. Угол α определим из треугольника АЕС: 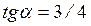 , тогда: α = 36,9º, и sin α = 0,6; cos α = 0,8.
, тогда: α = 36,9º, и sin α = 0,6; cos α = 0,8.
Составим уравнения равновесия:
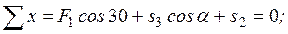
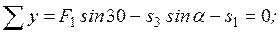
Решая эту систему уравнений, находим: s 3 = 11,254 кH, s 2 = -17,663 кH. Отрицательные значения усилий в первом и втором стержнях показывают, что эти стержни не растянуты, как предполагалось, а сжаты.
Далее можно рассмотреть равновесие узла Е и определить s 5, s 6. Из уравнения проекций на ось у для узла D, можно найти усилие в седьмом стержне – s 7. Уравнения равновесия для узла В должны обратиться в тождество, они являются уравнениями проверки.
 3. Определим усилия в стержнях 2,3,4 методом сечений. Рассечем ферму сечением I-I (рис. С3в), и составим уравнения равновесия для части фермы, лежащей слева от сечения.
3. Определим усилия в стержнях 2,3,4 методом сечений. Рассечем ферму сечением I-I (рис. С3в), и составим уравнения равновесия для части фермы, лежащей слева от сечения.
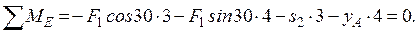 (4)
(4)
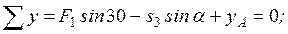 (5)
(5)
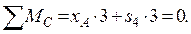 (6)
(6)
Из уравнения (4) находим s2 = -17,663 кH.
Из уравнения (5) находим s3 = 11,254 кH. Из уравнения (5) находим s4 = 16,309 кH.
Сравнивая эти результаты с полученными ранее, делаем вывод о том, что задача решена правильно.
Задача С4
Шесть невесомых стержней соединены своими концами шарнирно друг с другом в двух узлах и прикреплены другими концами (тоже шарнирно) к неподвижным опорам А, В, С, D (рис. С4.0-С4.9, табл. С4). Стержни и узлы (узлы расположены в вершинах Н, К, L, или М прямоугольного параллелепипеда) на рисунках не показаны и должны быть изображены решающим задачу по данным таблицы. В узле, который в каждом столбце таблицы указан первым, приложена сила Р=200 Н; во втором узле приложена сила Q=100 H. Сила 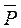 образует с положительными направлениями координатных осей х, y, z углы, равные соответственно: a1 = 45°, b1 = 60°, g1 = 60°, а сила Q – углы: a2 = 60°, b2 = 45°, g2 = 60°. Грани параллелепипеда, параллельные плоскости xy, - квадраты. Диагонали других (боковых) граней образуют с плоскостью xy угол j=60°, а диагональ параллелепипеда образует с этой плоскостью угол Q=51°. Определить усилия в стержнях.
образует с положительными направлениями координатных осей х, y, z углы, равные соответственно: a1 = 45°, b1 = 60°, g1 = 60°, а сила Q – углы: a2 = 60°, b2 = 45°, g2 = 60°. Грани параллелепипеда, параллельные плоскости xy, - квадраты. Диагонали других (боковых) граней образуют с плоскостью xy угол j=60°, а диагональ параллелепипеда образует с этой плоскостью угол Q=51°. Определить усилия в стержнях.
Указания. Задача С4 – на равновесие пространственной системы сходящихся сил. При ее решении следует рассмотреть отдельно равновесие каждого из двух узлов.
Таблица С4
| Номер условия | |||||
| Узлы | H, M | L, M | K, M | L, H | K, H |
| Стержни | HM, HA, HB, MA, MC, MD | LM, LA, LD, MA, MB, MC | KM, KA, KB, MA, MC, MD | LH, LC, LD, HA, HB, HC | KH, KB, KC, HA, HC, HD |
| Номер условия | |||||
| Узлы | M, H | L,H | K, H | L, M | K, M |
| Стержни | MH, MB, MC, HA, HC, HD | LH, LB, LD, HA, HB, HC | KH, KC, KD, HA, HB, HC | LM, LB, LD, MA, MB, MC | KM, KA, KD, MA, MB, MC |
 Рис. С4.0 Рис. С4.1
Рис. С4.0 Рис. С4.1

 Рис. С4.2 Рис. С4.3
Рис. С4.2 Рис. С4.3
Рис. С4.4 Рис. С4.5

Рис. С4.6 Рис. С4.7

Рис. С4.8 Рис. С4.9
Пример С4.
Конструкция состоит из невесомых стержней 1, 2, …,6, соединенных друг с другом (в узлах К и М) и с неподвижными опорами А, В, С, D шарнирами (рис. С4). В узлах К и М приложены силы 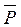 и
и 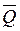 , образующие с координатными осями углы a1, b1, g1 и a2, b2, g2 соответственно (на рисунке показаны только углы a1, b1, g1).
, образующие с координатными осями углы a1, b1, g1 и a2, b2, g2 соответственно (на рисунке показаны только углы a1, b1, g1).
Дано: Р = 100 Н, a1 = 60°, b1 = 60°, g1 = 45°, Q = 50 H, a2 = 45°, b2 = 60°, g2 = 60°;
y = 30°, j = 60°, d ≈ 74°. Определить: усилия в стержнях 1 - 6.
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 2108; Нарушение авторских прав?; Мы поможем в написании вашей работы!