Теорема о параллельном переносе силы

Приведение системы сил к центру. Условия равновесия.

Равнодействующая системы сходящихся сил непосредственно находится с помощью закона параллелограмма сил.

В произвольной системы сил, т.е. системы в которой линии действия сил не пересекаются в одной точке, для определения равнодействующей требуется не только переносить силы вдоль линий их действия, но и параллельно им.

Поэтому используют следующую теорему: силу, приложенную к абсолютно твердому телу, можно, не изменяя оказываемого ею действия, переносить из данной точки в любую другую точку тела, прибавляя при этом пару с моментом, равным моменту переносимой силы относительно точки, куда сила переносится.

Пусть на твердое тело действует сила F, приложенная в точке А (рис. 37, а). Действие этой силы не изменяется "_если в любой точке В_ тела _приложить две уравновешенные силы F и J", такие, что F'=FJF"=—F. Полученная система трех сил и представляет собой силу F', равную F, но приложенную в точке В, и пару F F5 с моментом

Применяя данную теорему можно любую произвольную систему сил привести к одной Силе, равной их главному вектору и приложенной в центре приведения, и к паре сил с моментом, равным главному моменту всех сил относи­тельно центра приведения.

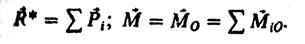
Выбор центра приведения не отражается на модуле и направлении лавного вектора R*, но влияет на модуль и направление главного мо­мента M₀. Поэтому всегда необходимо указывать относительно какого центра определяется главный момент.

ВОЗМОЖНЫЕ СЛУЧАИ ПРИВЕДЕНИЯ СИЛ, ПРОИЗВОЛЬНО РАСПОЛОЖЕННЫХ НА ПЛОСКОСТИ

При приведении сил, произвольно расположенных на плоскости, к заданному центру возможны следующие случаи:

Случай I. R*=0; М = М₀ = 0.

Если главный вектор системы сил равен нулю и ее главный момент относительно центра приведения тоже равен нулю, то силы взаимно уравновешиваются.

Случай II. R* = 0; М = М₀ ¹ 0.

Если главный вектор системы сил равен нулю, а ее главный момент относительно центра приведения не равен нулю, то силы приводятся к паре сил.

Момент этой пары, сил равен главному моменту системы сил относительно центра приведения.

В этом случае главные моменты данной системы сил относительно всех точек плоскости равны по модулю и совпадают по знаку

Случай III. R¹0; М = М₀ = 0.

Если главный вектор системы сил не равен нулю, а главный момент ее относительно центра приведения равен нулю, то силы приводятся к равнодействующей R = R*, линия действия которой проходит через центр приведения.

Случай IV. R¹0; М = M_O¹0.

В этом случае заданная система сил также приводится к одной силе - равнодействующей данной системы сил.

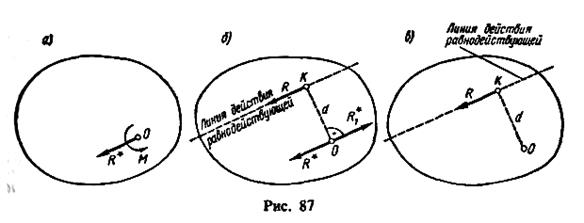
Выберем силы пары R*1, R равными по модулю R*. Тогда плечо этой пары следует взять равным d = M/R*.

Одну из сил пары KJ приложим в точке О, направив ее противоположно главному вектору R* (рис. 87, б). Тогда другая сила пары должна быть приложена в точке К отрезка ОК – d, отложенного перпендикулярно линии действия силы R*1 таким образом, чтобы пара R*1, R стремилась вращать плоскость чертежа в сторону, противоположную вращению часовой стрелки. Силы R* и R*1, приложенные в центре приведения О, как равные и противоположно направленные, уравновешиваются, и рассматриваемая система сил приводится к одной силе R, равной главному вектору сил и приложенной к точке К. Эта сила является равнодействующей данной системы сил (рис. 87, в).

На основе рассмотренных выше случаев приведения можно сделать следующий вывод.

Если силы, произвольно расположенные на плоскости, не уравновешиваются, то их можно привести или к одной силе, или к паре сил.

Если система сил имеет равнодействующую, то для определения суммы моментов сил относительно центра удобно использовать теорему Вариньона: если данная система сил имеет равнодействующую, то момент равнодействующей относительно любого центра О равен сумме моментов сил системы относительно того же центра.

ВОЗМОЖНЫЕ СЛУЧАИ ПРИВЕДЕНИЯ СИЛ, ПРОИЗВОЛЬНО РАСПОЛОЖЕННЫХ В ПРОСТРАНСТВЕ

При приведении сил, произвольно расположенных в пространстве, к заданному центру возможны следующие случаи:

Случай I. R* = 0; M = M₀ = 0.

Если главный вектор системы сил и ее главный момент относительно центра приведения равны нулю, то силы взаимно уравновеши­ваются.

Случай II. R* = 0;M=M₀¹0.

Если главный вектор системы сил равен нулю, а ее главный момент относительно центра приведения не равен нулю, то силы приводятся к паре сил.

Случай III. R¹0; М = М₀ = 0.

Если главный вектор системы сил не равен нулю, а ее главный момент относительно центра приведения равен нулю, то силы приводятся к равнодействующей R = R*, линия действия которой проходит через центр приведения.

С л у ч а и IV. R¹0; М = M_O¹0. и M_O^R*

показано, что если главный момент системы сил относительно центра приведения перпендикулярен главному вектору, то силы приводятся к равнодействующей силе R. = R*, линия действия которой не проходит через центр приведения.

Случай V. R¹0; М = M_O¹0. и M_O не ^R*

Ниже, в § 46, показано, что если главный момент системы сил относительно центра приведения не перпендикулярен главному вектору, то силы приводятся к двум скрещивающимся силам, или к силовому винту (динаме), т. е. к совокупности силы и пары сил, плоскость действия которой перпендикулярна силе.

Случаи I-IV возможны и при расположении сил в одной плоскости.

Дата добавления: 2015-06-04