Трение качения

ТРЕНИЕ

СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ И СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ ЗАДАЧИ

Статически определимыми называют задачи, которые можно решать методами статики твердого тела, т. е. задачи, в которых число неизвестных не превышает числа уравнений равновесия. Статически неопределимыми называют задачи с числом неизвестных, превышающим число уравнений равновесия сил, и для решения которых нужно учитывать деформации тела, обусловленные внешними нагрузками.

Для решения задач на равновесие произвольно расположенных на плоскости сил, приложенных к твердому телу, можно пользоваться тремя уравнениями равновесия сил. Задача статически определима, если число неизвестных не больше трех. Если к телу приложена плоская система параллельных сил, то можно воспользоваться только двумя уравнениями равновесия сил. Задача статически определима, если число неизвестных, в ней не превышает двух.

Для параллельных сил, приложенных к системе n тел, можно составить по два уравнения равновесия для сил, приложенных к каждому из этих тел, т. с. всего I*n уравнений равновесия. Если же на эту систему тел действуют силы, произвольно расположенные на плоскости, то общее число уравнений равновесия сил, приложенных к системе тел, равно Зn.

§23. ЗАКОНЫ ТРЕНИЯ СКОЛЬЖЕНИЯ

При стремлении двигать одно тело по поверхности другого в плоскости соприкосновения тел возникает сила трения скольжения.

Возникновение трения обусловлено, прежде всего, шероховатостью поверхностей, создающей сопротивление перемещению, и наличием сцепления у прижатых друг к другу тел.

В инженерных расчетах обычно исходят из ряда установленных опытным путем закономерностей, которые называют законами трения скольжения при покое:

•I. Сила трения может принимать любые значения от нуля до значения F_пр предельной силой трения.

Сила трения направлена в сторону, противоположную той, куда действующие на тело силы стремятся его сдвинуть.

2. Предельная сила трения численно равна произведению статического коэффициента трения на нормальное давление или нормальную реакцию:

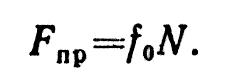
Статический коэффициент трения f₀ — величина безразмерная; он определяется опытным путем и зависит от материала соприкасающихся тел и состояния поверхностей (характер обработки, температура, влажность и т. п.).

3. Значение предельной силы трения в довольно широких пределах не зависит от размеров соприкасающихся при трении поверхностей.

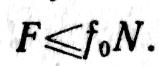
значение силы может быть любым, но не большим, чем F_np.

Все изложенное выше относилось к трению скольжения при покое. При движении сила трения направлена в сторону, противоположную движению, и равна произведению динамического коэффициента трения на нормальное давление:

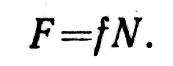
Динамический коэффициент трения скольжения f также является величиной безразмерной и определяется опытным путем. Значе­ние коэффициента зависит не только от материала и состояния поверхностей, но и в некоторой степени от скорости движущихся тел. В большинстве случаев с увеличением скорости коэффициент сначала несколько убывает, а затем сохраняет почти постоянное значение.

РЕАКЦИИ ШЕРОХОВАТЫХ СВЯЗЕЙ. УГОЛ ТРЕНИЯ

Реакция реальной (шероховатой) связи слагается из двух составляющих: из нормальной реакции N и перпендикулярной ей силы трения F. Следовательно, полная реакция R будет отклонена от

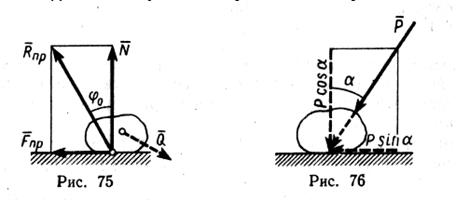
нормали к поверхности на некоторый угол. При изменении силы трения от нуля до Fnp сила R изменяется от N до Rпр, а ее угол с нормалью растет от нуля до некоторого предельного значения φ₀, Наибольший угол φ₀, который полная реакция шероховатой связи образует с нормалью к поверхности, называется углом трения.

При равновесии полная реакция R в зависимости от сдвигающих сил может проходить где угодно внутри угла трения. Когда равновесие становится предельным, реакция будет отклонена от нормали на угол ф0.

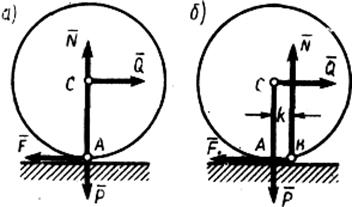
Трением качения называется сопротивление, возникающее при качении одного тела по поверхности другого.

Вследствие деформаций тел касание их происходит вдоль некоторой площадки АВ (б). При действии силы Q интенсивность давления у края А убывает, а у края В возрастает. В результате реакция N оказывается смещенной в сторону действия силы Q. С увеличением Q это смещение растет до некоторой предельной величины k. Таким образом, в предельном положении на каток будут действовать пара Q_np, F с моментом Q_прR и уравновешивающая ее пара N, Р с моментом Nk. Из равенства моментов находим

Qпр=(k/R)N. (43)

Пока Q<Qnp, каток находится в покое; при Q>Qnp начинается качение.

Входящая в формулу (43) линейная величина k называется коэффициентом трения качения. Измеряют величину k обычно в сантиметрах. Значение коэффициента k зависит от материала тел и определяется опытным путем.

Отношение k/R для большинстве материалов значительно меньше статического коэффициента трения f₀- Этим объясняется то, что в технике, когда это возможно, стремятся заменить скольжение качением (колеса, катки, шариковые подшипники и т. п.).

Дата добавления: 2015-06-04