Виды типовых воздействий в САУ

Характеристическое уравнение звена

Пример 2

Пример 1

Передаточная функция звена.

Применив преобразование Лапласа к дифференциальному уравнению звена

a_n+a_n-1+...+a₁+a₀y(t) = b_m+b_m-1+...+b₁+b₀x(t),

получим

a_npⁿY(p)+a_n-1p^n-1Y(p)+...+a₁pY(p)+a₀Y(p) = b_mp^mX(p)+b_m-1p^m-1X(p)+...+b₁pX(p)+b₀X(p).

Если вынести общие множители Y(p) и X(p), имеем:

Y(p)(a_npⁿ+a_n-1p^n-1+...+a₁p+a₀)=X(p)(b_mp^m+b_m-1p^m-1+...+b₁p+b₀).

Передаточной функцией звена W(р) называется отношение изображений Лапласа выходной и входной величин звена при нулевых начальных условиях т. е.:

W(р)=; или W(р)=.

Между дифференциальными уравнениями и передаточными функциями существует однозначная связь. Сравнивая последнее выражение с дифференциальным уравнением звена, видим, что формально передаточную функцию звена можно составлять как отношение операторных многочленов правой и левой частей уравнения звена. И наоборот, зная передаточную функцию, легко написать его уравнение, имея в виду что числитель передаточной функции соответствует правой части уравнения, а знаменатель передаточной функции — левой части уравнения.

В теории автоматического регулирования принято приводить уравнение звена к стандартному виду, когда свободный член равен единице:

W(р)=×=k×,

где через An(p) и Bm(p) обозначены многочлены относительно р с коэффициентами 1 в младших членах, причем степень Bm(p), как правило, ниже степени An(p), т. е. m<n;

k= – коэффициент усиления звена.

Пусть звено описывается дифференциальным уравнением

T2+T1+y(t)=kx(t).

В операторной форме уравнение имеет вид

Y(p)(T2p2+T1p+1)=kX(p).

Откуда передаточная функция звена

W(p)==.

Решим обратную задачу - найдем по передаточной функции дифференциальное уравнение.

Пусть передаточная функция имеет вид:

W(p)==,

откуда

Y(p)(Tp+1)=kX(p);

TpY(p)+Y(p)=kX(p).

Учитывая, что pº (формальное операционное соответствие), получим:

T+y(t)=kх(t).

Многочлен в знаменателе передаточной функции звена A_n(p) называют характеристическим полиномом.

Характеристическое уравнение звена имеет вид:

A_n(p)=0, или A_npⁿ+A_n-1p^n-1+...+A₁p+1=0,

так что корни p_i характеристического уравнения звена являются полюсами его передаточной функции.

При анализе работы систем автоматического регулирования и их отдельных элементов в качестве типовых выбирают одно из следующих возмущений.

Импульсное возмущение — возмущение, полученное как последовательность двух одинаковых по величине, но противоположных по знаку ступенчатых возмущений, сдвинутых во времени на величину, обратную величине их интенсивности (рис.3б). Особое значение имеет единичная импульсная функция или дельта-функция, обозначаемая d(t).

Дельта-функция обладает следующими свойствами:

d (t)= , .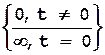

Первое свойство означает, что дельта-функция существует лишь в момент времени t=0. Второе свойство означает, что, несмотря на пренебрежимо малую длительность функции, площадь, ограниченная ею, имеет конечное значение, равное единице. Единичная импульсная функция является производной от единичного скачка, т. е.:

d(t)=.

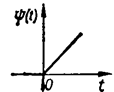
Ступенчатое возмущение — мгновенное изменение воздействия на постоянную величину, чаще всего равную единице (рис.3а). Физическая система испытывает толчок. Аналитически ступенчатое возмущение записывается в виде

f(t)= .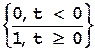

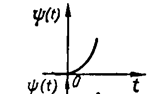г д

а — ступенчатое; б — импульсное; в — гармоническое; г — скачок скорости; д — скачок ускорения

Рис.3. Типовые возмущения систем.

Периодическое возмущение — возмущение, изменяющееся периодически во времени. Оно удобно для исследования автоматических систем, работающих в режиме незатухающих колебаний. Наиболее простым периодическим возмущением является гармоническое колебание единичной амплитуды (рис. 3в).

Скачок скорости или скачок ускорения — возмущения, являющиеся стандартными для следящих систем, которые работают в режиме постоянной скорости x(t)=at (рис.3г) или постоянного ускорения x(t)=bt² (рис.3д).

Дата добавления: 2015-06-25