
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Инерционное (апериодическое) звено
|
|
|
|
Уравнение и передаточная функция звена:
(Тр+1)Y(p)=kX(p); W(p)=,
где Т – постоянная времени; k – коэффициент передачи звена.
Примерами инерционных (апериодических) звеньев являются двигатели постоянного тока, если х(t) — напряжение питания, а y(t) — угловая скорость вала w(t); двухфазные асинхронные двигатели; усилители при учете инерционного запаздывания; массивное тело, если входной величиной считать количество поступающего в единицу времени тепла Q, а выходной — температуру в какой-либо точке внутри тела и др.); L-R цепочка (рис.11).
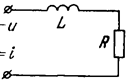
Рис.11. Пример инерционного звена.
Амплитудно-фазовая частотная характеристика: W(jw)= (рис.12).
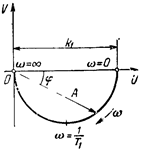
Рис.12. АФЧХ инерционного звена.
Из W(jw) находим: A(w)=, y(w)=-arctgwT.

Рис.13. Амплитудно-частотная и фазо-частотная характеристики инерционного звена
Логарифмическая амплитудно-частотная характеристика имеет вид:
L(w)=20lg=20lgk-20lg.
Эта характеристика имеет асимптоты:
а)при w®0 L(w)®20lgk;
б)при w®¥ L(w)®20lgk-20lgTw.
Последняя асимптота будет наклонной прямой с наклоном -20 дБ/дек, а первая – горизонтальная прямая. Пересекаются асимптоты в точке wс=. Сама ЛАЧХ близка к этим асимптотам.
На логарифмической сетке по оси частот откладывается сопрягающая частоте wс= (рис.14). Для частот меньших, чем сопрягающая, т. е. при w<, можно пренебречь вторым слагаемым под корнем, тогда левее сопрягающей частоты можно заменить L(w) приближенным выражением
L(w)»20lgk.
Этому выражению соответствует горизонтальная прямая. Для частот больших сопрягающей w> в выражении для L(w) можно пренебречь 1 под корнем. Тогда L(w)=20lgk-20lg(wT). Второе слагаемое представляет собой прямую линию, идущую под наклоном -20 дБ/дек. Ломаная линия и называется асимптотической ЛАЧХ. Наибольшее отклонение точной ЛАЧХ от асимптотической приблизительно равно 3 дБ на частоте сопряжения, т. к.:
DL()=20lgk-20lg=20lgk-3,03 (дБ).

Рис.14. ЛАЧХ инерционного звена.
Переходная функция, согласно решению уравнения звена, при х(t)=1(t) и нулевых начальных условиях имеет вид (рис.15):
h(t)=k  .
.
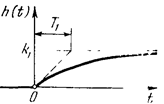
Рис.15. Переходная функция инерционного звена.
Постоянная времени Т определяет наклон касательной в начале кривой (рис.15). Следовательно, величина Т характеризует степень инерционности звена, т.е. длительности переходного процесса. Теоретически такой переходный процесс длится бесконечно долго. Практически для этого звена под временем переходного процесса понимают промежуток времени tп по истечении которого выполняется неравенство:
1-h(tп)£D,
где D - наперед заданное положительное число (обычно D=0,01¸0,05).
При подаче на вход звена постоянного сигнала x0 по окончании переходного процесса координата y(t) жестко связана с входной:
yуст=y(¥)=kx0.
|
|
|
|
|
Дата добавления: 2015-06-25; Просмотров: 961; Нарушение авторских прав?; Мы поможем в написании вашей работы!