КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Приведение пространственной системы сил к простейшему виду
|
|
|
|
Как было рассмотрено ранее (7.2) любая система сил проводится в общем случае к силе, равной главному вектору 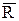 и приложенной в произвольном центру О, и к паре сил с моментом, равным главному моменту
и приложенной в произвольном центру О, и к паре сил с моментом, равным главному моменту 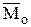 (рисунок 6.2 б). Найдем к какому простейшему виду может быть приведена произвольная пространственная система сил, не находящаяся в равновесии.
(рисунок 6.2 б). Найдем к какому простейшему виду может быть приведена произвольная пространственная система сил, не находящаяся в равновесии.
Вспомним теорему о параллельном переносе силы из точки А в точку В: (рисунок 10.4).

Рисунок 10.4
При переносе силы из точки А в точку В кроме силы 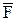 появляется пара сил, вектор-момент которой
появляется пара сил, вектор-момент которой 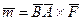 , но в тоже самое время величина
, но в тоже самое время величина 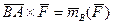 , т.е. при параллельном переносе силы
, т.е. при параллельном переносе силы 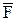 из одной точки пространства в другую к силе
из одной точки пространства в другую к силе 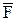 необходимо добавить пару сил, вектор-момент которой равен вектору-моменту данной силы относительно точки, в которую она переносится.
необходимо добавить пару сил, вектор-момент которой равен вектору-моменту данной силы относительно точки, в которую она переносится.
Таким образом, результат приведения произвольной пространственной системы сил зависит от значений, которые у этой системы сил имеют главный вектор 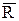 и главный момент
и главный момент 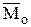 .
.
1) если для данной системы сил 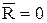 , а
, а 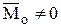 , то она приводится к паре сил, момент которой равен
, то она приводится к паре сил, момент которой равен 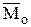 и может быть вычислен по формулам:
и может быть вычислен по формулам:
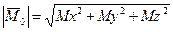 (10.7)
(10.7)
 ;
; 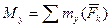 ;
; 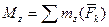 (10.8)
(10.8)
В этом случае значение 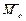 от выбора центра О не зависит.
от выбора центра О не зависит.
2) если для данной системы сил 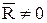 , а
, а 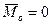 , то она приводится к равнодействующей, равной
, то она приводится к равнодействующей, равной 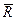 , линия действия которой проходит через центр О, в этом случае значение
, линия действия которой проходит через центр О, в этом случае значение 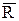 можно найти по формулам:
можно найти по формулам:
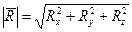 , (10.9)
, (10.9)
где
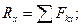
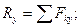
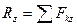 (10.10)
(10.10)
3) если для данной системы сил 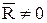 , а
, а 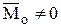 , но
, но  , то эта система также приводится к равнодействующей, равной
, то эта система также приводится к равнодействующей, равной 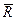 , но не проходящей через центр О. (рисунок 10.5)
, но не проходящей через центр О. (рисунок 10.5)
|

рисунок 10.5
В этом случае пара сил 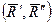 , изображаемая вектором
, изображаемая вектором 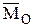 и сила
и сила 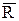 лежат в одной плоскости. Если выбрать силы
лежат в одной плоскости. Если выбрать силы 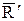 и
и 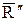 по модулю равными силе
по модулю равными силе 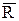 , то получим, что силы
, то получим, что силы 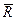 и
и 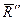 взаимно уравновесятся и система заменится одной равнодействующей
взаимно уравновесятся и система заменится одной равнодействующей 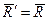 , линия действия которой проходит через точку
, линия действия которой проходит через точку 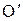 , где
, где 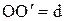 - (плечо пары). Этот случай будет иметь место для любой системы параллельных сил или сил, лежащих в одной плоскости, если главный вектор этой системы
- (плечо пары). Этот случай будет иметь место для любой системы параллельных сил или сил, лежащих в одной плоскости, если главный вектор этой системы 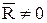 .
.
4) если для данной системы сил 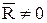 ,
, 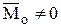 , при этом вектор
, при этом вектор 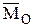 параллелен
параллелен 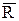 (рисунок 10.6 а), то это означает, что система сил приводится к совокупности силы
(рисунок 10.6 а), то это означает, что система сил приводится к совокупности силы 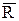 и пары
и пары 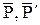 , лежащей в плоскости, перпендикулярной силе (рисунок 10.6 б). Такая совокупность силы и пары называется динамическим винтом, а прямая, вдоль которой направлен вектор
, лежащей в плоскости, перпендикулярной силе (рисунок 10.6 б). Такая совокупность силы и пары называется динамическим винтом, а прямая, вдоль которой направлен вектор 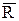 , осью винта.
, осью винта.

Рисунок 10.6
5) если для данной системы сил 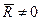 ,
,  , при этом вектор
, при этом вектор 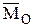 и
и 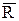 не перпендикулярны друг другу и не параллельны, то такая система сил тоже приводится к динамическому винту, но ось винта не будет проходит через центр О.
не перпендикулярны друг другу и не параллельны, то такая система сил тоже приводится к динамическому винту, но ось винта не будет проходит через центр О.
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 1894; Нарушение авторских прав?; Мы поможем в написании вашей работы!