Момент силы относительно оси. Ранее в разделе 5.1 было введено понятие о моменте силы относительно центра О

Ранее в разделе 5.1 было введено понятие о моменте силы относительно центра О. Это вектор 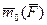, направленный перпендикулярно плоскости ОАВ (рисунок 10.2), модуль которого имеет значение 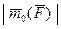= 2 площади .

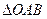Рисунок 10.1

Моментом силы относительно оси Z называется проекция момента силы 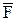относительно центра О, лежащего на оси Z, на эту ось, т.е.

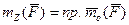или 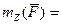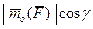(10.1)

где 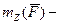момент силы 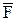относительно оси Z; 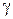- угол между вектором 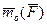и осью Z.

Из определения следует, что 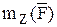, как проекция вектора на ось, является алгебраической величиной, знак которой определяется также как знак проекции любого вектора.

Из рисунка 10.1 следует, что если менять положении точки O на оси Z, то и модуль, и направление вектора 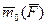будут при этом изменяться, но 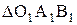, а с ним и значение 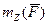изменяться не будут.

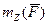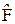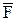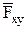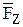Механический смысл величины состоит в том, что она характеризует вращательный эффект силы , когда эта сила стремится повернуть тело вокруг оси Z. Если же разложить силу на составляющие и , где 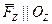(рисунок 10.2), то поворот вокруг оси Z будет совершать только составляющая 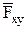и вращательный эффект всей силы 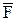будет определяться величиной

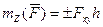(10.2)

Составляющая же 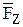может только сдвинуть тело вдоль оси Z.

Рисунок 10.2

В заключение рассмотрим подробнее, как вычисляется момент силы относительно оси Z по формуле (10.2). Для этого надо (рисунок 10.2):

1) провести плоскость ХУ, перпендикулярную оси Z, через произвольную точку О, расположенную на оси Z;

2) спроектировать силу 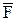на эту плоскость и найти величину ;

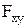3) опустить из точки пересечения оси с плоскостью (т. О) перпендикуляр h на линию действия силы 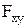и найти длину h;

4) вычислить произведение ;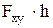

5) определить знак момента, пользуясь правилом: момент силы относительно оси, будет иметь знак плюс, когда с положительного конца оси поворот, который стремиться совершить сила 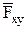, виден происходящим против часовой стрелки, и знак минус – когда по ходу часовой стрелки.

При вычислении моментов могут иметь место следующие частные случаи:

1) если сила параллельна оси, то ее момент относительно оси равен нулю. (т.к. 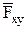= 0);

2) если линия действия силы пересекает ось, то ее момент относительно оси так же равен нулю (т.к. h = 0).

Таким образом, момент силы относительно оси равен нулю, если сила и ось лежат в одной плоскости.

3) если сила перпендикулярна оси, то ее момент относительно оси равен взятому с соответствующим знаком произведению модуля силы на расстояние между линией действия силы и осью.

Пример:

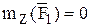; т.к. 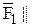оси Z.

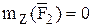; т.к. 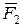пересекает ось Z.

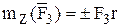
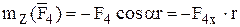
Дата добавления: 2015-06-04