
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Демонстрационные примеры. Вопросы для теоретической подготовки
|
|
|
|
Вопросы для теоретической подготовки
Тема 5. Дискретная случайная величина
Ø Цель: привить навыки использования различных законов распределения дискретных случайных величин.
1.Что называется дискретной случайной величиной (дсв) и ее рядом распределения?
2.Что называется биномиальным законом распределения и в каком случае он используется?
3.Как определяется закон распределения Пуассона? Наивероятнейшее число появлений события.
4.Что называется потоком случайных событий? Какой поток называется простейшим и какими свойствами обладает?
5.Что называется геометрическим и гипергеометрическим распределением, и в каком случае они используются?
Пример 1. Два равносильных шахматиста играют в шахматы. Что вероятнее: выиграть две партии из четырех или три партии из шести (ничьи во внимание не принимаются)?
Решение. Играют равносильные шахматисты, поэтому вероятность выигрыша р = 0,5; следовательно, вероятность проигрыша такая же q = 0,5. Так как во всех партиях вероятность выигрыша постоянна и не зависит от результата предыдущих партий, то применима формула Бернулли. Вероятность того, что будут выиграны две партии из четырех,
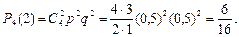
а вероятность того, что будут выиграны три партии из шести,
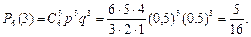
Так как Р 4(2) > Р 6(3), то вероятнее выиграть две партии из четырех, чем три партии из шести.
Пример 2. Станок-автомат штампует детали. Вероятность того, что изготовленная деталь окажется бракованной, равна 0,01. Найти вероятность того, что среди 200 деталей окажется ровно четыре бракованных.
Решение. По условию, р = 0,01, n = 200, l = np = 2, k = 4. Воспользуемся формулой Пуассона
P (k) = (l) k×e–l/k! = 24× e –2/4! = 16× e –2/24 = 0,09.
Пример 3. Среднее число вызовов, поступающих на АТС в одну минуту, равно двум. Найти вероятность того, что за 5 минут поступит:
а) 2 вызова; б) менее двух вызовов; в) не менее двух вызовов. Поток вызовов предполагается простейшим.
Решение. По условию, l = 2, t = 5, k = 2. Воспользуемся формулой Пуассона для потока событий интенсивности l: вероятность поступления k заявок за время t
Pt (k) = (lt) k×e–lt/k!.
Искомая вероятность, что за 5 минут поступят 2 вызова,
P 5(2) = (10)2× e –10/2! = 0,00227.
По теореме сложения вероятностей несовместных событий
P 5(k < 2) = P 5(0) + P 5(1) = e –10 + 10× e –10/1! = 0,000495.
События «поступило менее двух вызовов» и «поступило не менее двух вызовов» противоположны. Поэтому искомая вероятность
P 5(k ³ 2) = 1 – P 5(k < 2) = 0,999505.
Пример 4. Каждый из 15 банков проходит аудиторскую проверку. Вероятность того, что банк выдержит испытание, равна 0,9. Найти наивероятнейшее число банков, которые выдержат испытание.
Решение. По условию, n = 15, р = 0,9, q = 0,1. Найдем наивероятнейшее число k 0 из двойного неравенства
np – q £ k 0 £ np + p.
Подставив данные примера, получим
15×0,9 – 0,1 £ k 0 £ 15×0,9 + 0.9 или 13,4 £ k 0 £ 14,4.
Так как k 0 - целое, то искомое наивероятнейшее число k 0 = 14.
Задания для самостоятельного решения
1. В цехе 6 моторов. Для каждого мотора вероятность того, что он в данный момент включен, равна 0,8. Какова вероятность того, что в данный момент:
а) включено 4 мотора. (0,246);
б) включены все моторы. (0,26);
в) выключены все моторы? (0,000064).
2. На автобазе имеется 12 автомашин. Вероятность выхода на линию каждой из них равна 0,8. Найти вероятность нормальной работы автобазы, если для этого необходимо иметь на линии 8 автомашин. (0,9274).
3. Какова вероятность того, что объект будет поражен при пяти независимых выстрелах, если для этого необходимо не менее двух попаданий? Вероятность попадания при каждом выстреле равна 0,3. (0,472).
4. Учебник издан тиражом 100 000 экземпляров. Вероятность того, что учебник сброшюрован неправильно, равна 0,0001. Найти вероятность того, что тираж содержит ровно пять бракованных книг. (0,0375).
5. Среднее число покупателей, прибывающих в супермаркет за 1 мин, равно 5. Какова вероятность того, что за 2 мин прибудет:
а) ровно два покупателя. (0,00227);
б) менее двух покупателей. (0,000495);
в) не менее двух покупателей? (0,999505).
6. Вероятность попадания стрелком в цель равна 0,7. Сделано 25 выстрелов. Определить наивероятнейшее число попаданий в цель. (18).
7. В результате многолетних наблюдений установлено, что вероятность выпадения дождя 1 октября в данном городе равна 1/7. Определить наивероятнейшее число дождливых дней 1 октября в данном городе за 40 лет. (5).
8. Товаровед осматривает 24 образца товаров. Вероятность того, что каждый из образцов будет признан годным к продаже, равна 0,6. Найти наивероятнейшее число образцов, которые товаровед признает годными к продаже. (14 и 15).
9. Из орудия производится стрельба по цели до первого попадания. Вероятность попадания в цель р = 0,6. Какова вероятность того, что попадание произойдет при третьем выстреле? (0,096).
10. Среди 50 изделий 20 импортных. Какова вероятность того, что среди наудачу извлеченных 5 изделий ровно 3 импортных? (0,234).
|
|
|
|
|
Дата добавления: 2015-06-25; Просмотров: 1490; Нарушение авторских прав?; Мы поможем в написании вашей работы!