Демонстрационные примеры

Вопросы для теоретической подготовки

1. Сформулировать правило суммы и произведения.

2. Размещения с повторениями и без повторений. привести примеры задач.

3. Перестановки с повторениями, ограничениями и без повторений.

4. Сочетания с повторениями и без повторений.

5. Раскладка элементов по ящикам. Раздел предметов на две группы.

6. Распределение одинаковых предметов на любое количество групп.

7. Задача о смещении.

Пример 1. В колоде 36 карт. Каким количеством способов можно выбрать либо одного туза, либо один козырь?

Решение. Искомое количество равно сумме способов, которыми можно выбрать один туз и один козырь. Один некозырный туз можно выбрать тремя способами, а один козырь – девятью способами. Поэтому либо туз, либо козырь можно выбрать 12 способами (правило суммы).

Пример 2. В колоде 36 карт. Каким количеством способов можно выбрать две карты: одного туза и один козырь?

Решение. Искомое количество равно произведению количества способов, которыми можно выбрать один туз и один козырь. Один некозырный туз можно выбрать тремя способами, а один козырь – девятью способами. Поэтому искомые две карты можно выбрать 27 способами (правило произведения).

Пример 3. Номера лотерейных билетов состоят из 7 цифр. Сколько билетов можно пустить в тираж?

Решение. Искомое количество равно произведению количества способов, которыми можно заполнить каждую из 7 цифр номера билета (правило произведения). Номера билетов образуют 7 размещений с повторениями из 10 возможных цифр, так как цифры могут повторяться. Число всех таких возможных размещений обозначается через

Пример 4. В олимпиаде участвуют 30 студентов. Сколькими способами могут распределиться первые 3 места?

Решение. Искомое количество равно произведению количества способов, которыми можно заполнить каждое место (правило произведения). Поскольку эти места могут быть заняты разными студентами, то перемножаются числа 30×29×28. Это количество называется тремя размещениями без повторений из 30 возможных студентов и обозначается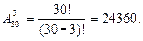

Пример 5. Сколько различных расположений букв можно получить из букв слова «ИЗОТЕРМА»?

Решение. Искомое количество равно произведению количества способов, которыми можно заполнить каждое из 8 мест для буквы (правило произведения). Поскольку эти места могут быть заняты разными буквами, то перемножаются числа 8×7×6×5×4×3×2×1. Это число называется числом перестановок из 8 букв и обозначается Р ₈ = 8! = 40320.

Пример 6. Сколько различных расположений букв можно получить из букв слова «МАТЕМАТИКА»?

Решение. В данном слове 10 букв, причем буква «А» повторяется три раза, а буквы «М» и «Т» по два раза. Поэтому в каждой перестановке, меняя местами буквы «А» или «М» или «Т», мы не получим новых комбинаций (перестановки с повторениями). Число различных расположений букв будет в 3! ×2!×2! раза меньше. Искомое количество равно числу перестановок из 10 букв, деленное на число перестановок каждой из повторяющихся букв

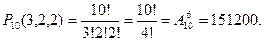
Пример 7. Сколько различных расположений букв можно получить из букв слова «ИЗОТЕРМА» так, чтобы никакие две гласные не стояли рядом?

Решение. Такие расположения букв называются перестановками с ограничениями. Найдем сначала количество возможных способов расположения гласных. Поскольку в данном слове 4 согласных, то существует всего 5 мест расположения гласных: 3 места между согласными и 2 – по краям слова. Поэтому количество всех способов равно числу размещений 4 гласных на 5 возможных мест.

Это количество необходимо умножить на количество перестановок 4 согласных (правило произведения). То есть число различных расположений букв равно

Пример 8. Сколькими способами можно выбрать 4 сорта из 10 имеющихся в продаже сортов мороженого?

Решение. Варианты выбора считаются разными, если содержат разные сорта мороженого. Поэтому рассматриваются сочетания из 10 сортов по 4 сорта, которые вычисляются по формуле

Пример 9. Сколькими способами можно выбрать 4 порции мороженого, если в продаже имеется 10 сортов мороженого?

Решение. Варианты выбора считаются разными, если содержат разные количества мороженного одного сорта. Поэтому рассматриваются сочетания с повторениями из 10 сортов по 4 порции, которые обозначаются буквой «С» с черточкой и вычисляются по формуле

Замечание. Представим каждый сорт мороженого в виде одной из 10 возможных позиций, разделы между которыми изобразим буквой «Р». Итого получится 9 букв «Р». Каждую порцию мороженого представим в виде буквы «М». получится слово из 13 букв, в котором всего две разные буквы: «Р» повторяется 9 раз, а буква «М» – 4 раза. Количество способов выбора 4 порций мороженого равно числу различных расположений букв, входящих в рассматриваемое слово. Искомое количество равно числу перестановок из 13 букв, деленное на число перестановок каждой из повторяющихся букв

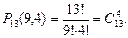
Пример 10. В колоде 36 карт. Сколькими способами можно раздать по 6 карт 4 игрокам?

Решение. Расположим все 36 карт в ряд и будем считать, что первые 6 карт достались первому игроку, вторые 6 карт – второму, третьи 6 карт – третьему, четвертые 6 карт – четвертому игроку, а остальные 12 карт остались в колоде. Тогда различным раскладкам соответствуют такие перестановки карт в этом ряду, которые меняют состав одной из четырех шестерок или 12 последних карт. В этом случае перестановки внутри шестерок и между картами колоды не меняют расклада. Поэтому количество различных перестановок из 36 карт будет больше количества разных раскладов в 6! × 6! × 6!× 6! × 12! раз. Поэтому количество разных раскладов

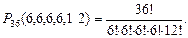
Пример 11. У двух ребят есть 10 яблок, 15 апельсинов и 14 груш.

1. Сколькими способами они могут разделить эти фрукты между собой?

2. Как изменится количество способов раздела, если каждому ребенку достанется не менее двух фруктов каждого вида?

Решение. Яблоки можно разделить 11 способами, апельсины – 16 способами и груши – 15 способами. Согласно правилу произведения все эти способы перемножаются 11 ×16 ×15 = 2640 способов.

Во втором случае в разделе участвуют 10 – 4 = 6 яблок, 15 – 4 = 11 апельсинов и 14 – 4 = 10 груш. Поэтому число различных разделов равно 7 ×12 ×11 = 924.

Пример 12. У трех ребят есть 40 яблок. Сколькими способами они могут разделить все яблоки между собой?

Решение. Представим каждого из 3 ребят как возможную позицию для размещения яблок, разделы между которыми изобразим буквой «Р». Итого получится 2 буквы «Р». Каждое яблоко представим в виде буквы «Я». получится слово из 42 букв, в котором всего две разные буквы: «Р» повторяется 2 раза, а буква «Я» – 40 раз. Количество способов раздела 40 яблок равно числу различных расположений букв, входящих в рассматриваемое слово. Искомое количество равно числу перестановок из 42 букв, деленное на число перестановок каждой из повторяющихся букв

Пример 13. Берутся все перестановки из 5 чисел 1, 2, 3, 4, 5. Найти количество перестановок N, в которых ни одно из этих чисел не остается на месте.

Решение. Представим это количество как разность всех перестановок Р ₅ и количества перестановок Р ₄, в которых одно из чисел стоит на своем месте. Таких чисел будет 5 = 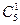. Однако мы вычли слишком много перестановок, так как среди них попадаются и такие, в которых другое число тоже стоит на своем месте. Поэтому к полученной разности необходимо добавить количество перестановок Р ₃, в которых два числа стоят на своих местах. Таких пар чисел будет 10 = . И так далее. Таким образом, искомое количество представляется в виде

.

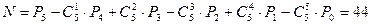Задания для самостоятельного решения

1. Из 3 групп студентов нужно выбрать одного участника олимпиады по математике. Каким количеством способов это можно сделать, если в первой группе 10 студентов увлекаются математикой, во второй – только 5 студентов, а в третьей – 7 студентов? (22).

2. Из 2 групп студентов нужно выбрать 2 участников олимпиады, в которой предлагаются задания по математике и информатике. Каким количеством способов это можно сделать, если в первой группе 12 студентов увлекаются математикой, а во второй – 10 студентов увлекаются информатикой? (120).

3. Сколько существует способов задать на компьютере код, состоящий из 4 букв русского алфавита? (33⁴ = 1185921).

4. На денежных знаках печатается индекс, состоящий из 2 букв русского алфавита и семи цифр от 0 до 9 каждая. Сколько сторублевых купюр можно напечатать, чтобы индекс был разным? (10 890 000 000).

5. Путем опроса общественного мнения изучается рейтинг 10 политиков. Сколькими способами могут распределиться первые четыре места? (5040).

6. Флаг страны состоит из 3 разноцветных горизонтальных полос. Сколько стран могут иметь такой флаг, если участвуют 7 цветов спектра и белый цвет? (336).

7. На собрании должны выступить 5 человек. Сколькими способами можно составить список выступающих? (120).

8. Сколькими способами можно составить кортеж президента, если он состоит из 3 «мерседесов», 4 «БМВ» и 5 мотоциклов? (27720).

9. В очереди стоят 5 мужчин и 4 женщины. Сколько разных очередей можно составить, если женщины не стоят в очереди друг за другом? (43200).

10. На телеканал ОРТ поступило 10 реклам, среди которых 4 рекламы зубной пасты. Сколькими способами можно составить очередность показа этих реклам, чтобы никакие две рекламы зубной пасты не шли одна за другой? (25200).

11. Команда по мини-футболу состоит из 10 футболистов. Сколькими способами можно выбрать основной состав из 6 игроков? (210).

12. Для проведения вступительного экзамена создается комиссия из 3 математиков и 2 экономистов. Сколькими способами можно составить комиссию, если в вузе работает 10 математиков и 12 экономистов? (7920).

13. Два филателиста решили обменять 3 марки. Сколькими способами это можно сделать, если первый филателист приготовил для обмена 12 марок, а второй – 10 марок? (26400).

14. В колоде 36 карт. Сколькими способами можно набрать 21 очко, выбрав 3 карты, если валет имеет 2 очка, дама – 3 очка, король – 4 очка, а туз – 11 очков? (564).

15. В кондитерском магазине продаются 4 вида пирожных: заварные, песочные, слоеные и корзинка. Сколькими способами можно купить 6 пирожных? (84).

16. На первом этаже 9-этажного дома в лифт вошли 4 человека. Сколькими способами они могут выйти, если лифт останавливается только на первых 8 этажах? (210).

17. При игре в домино 4 игрока делят поровну 28 костей. Сколькими способами они могут это сделать? (28!/(7!)⁴).

18. Для проверки 4 объектов прибыла комиссия из 8 человек. Сколькими способами можно распределить членов комиссии по два человека на каждый объект? (2520).

19. Двое грибников собрали 10 подберезовиков, 10 белых грибов и 15 подосиновиков. Сколькими способами они могут разделить эти грибы, чтобы каждому грибнику досталось не менее 3 грибов каждого вида? (250).

20. У воспитателя в детском саду было 100 конфет. Сколькими способами можно разделить конфеты, если в группе 20 детей, и каждому должно достаться не менее 3 конфет? (С⁴⁰₅₉).

21. Почтальон должен разнести 5 разных газет, но не поставил на них адреса и разнес их наугад. Найти количество возможных случаев, в которых только две газеты попали по адресу (20).

22. Шесть человек взяли из колоды по одной карте. Затем все эти карты перемешали и раздали снова. Сколько существует вариантов раздачи, в которых ни один не получил ту же карту, которую вытащил вначале (265)?

Дата добавления: 2015-06-25