Демонстрационные примеры. Вопросы для теоретической подготовки

Вопросы для теоретической подготовки

И числовые характеристики

Тема 7. Непрерывная случайная величина

Ø Цель: научить вычислять числовые характеристики непрерывной случайной величины и использовать их свойства.

1. Чем отличается непрерывная случайная величина (нсв) от дискретной? Что называется функцией распределения нсв?

2. Свойства функции и плотности распределения нсв.

3. Формулы вычисления математического ожидания и дисперсии нсв.

4. Нормальный закон распределения, его параметры и вероятностный смысл.

5. Центральная предельная теорема Ляпунова.

6. Нормальная кривая и ее свойства.

7. Вероятность попадания нормальной случайной величины в заданный интервал. Функция Лапласа и ее свойства. Вероятность заданного отклонения. Правило трех сигм.

8. Начальный и центральный момент к -го порядка.

9. Асимметрия и эксцесс, медиана и мода случайной величины.

Пример 1. Найти математическое ожидание и дисперсию случайной величины Х, заданной функцией распределения

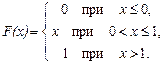
Вычислить вероятность того, что случайная величина Х примет значение в интервале (0,5; 2).

Решение. Найдем плотность распределения:

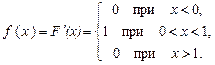
Найдем математическое ожидание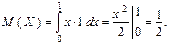

Найдем дисперсию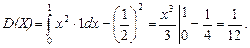

Вычислим вероятность Р (0,5 < Х < 2) = F (2) – F (0,5) = 1 – 0,5 = 0,5.

Пример 2. Случайная величина Х распределена по нормальному закону с параметрами m, s. Найти вероятность попадания этой случайной величины в заданный интервал (a, b), если m = 30; s = 10; a = 10; b = 50. Изобразить на графике функции плотности найденную вероятность.

Решение. Искомая вероятность вычисляется по формуле

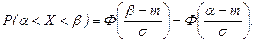
где F (х) – функция Лапласа. Для заданных значений параметров

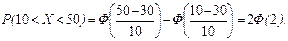
По таблице приложения Б находим F (2) = 0,4772. Отсюда искомая вероятность Р (10 < X < 50) = 2×0,4772 = 0,9544.

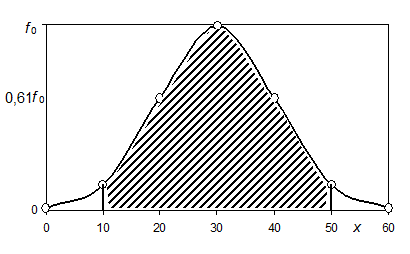
Рисунок 2 – Нормальная кривая с параметрами (30; 10)

На рисунке 2 площадь заштрихованной фигуры равна найденной вероятности.

Задания для самостоятельного решения

1. Найти математическое ожидание и дисперсию случайной величины Х, заданной функцией распределения

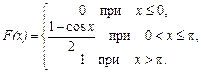
Вычислить вероятность того, что случайная величина Х примет значение в интервале (–0,5; p/2). (p/2; (p² – 8)/4; 0,5).

2. Случайная величина Х распределена по нормальному закону с параметрами m, s. Найти вероятность попадания этой случайной величины в заданный интервал (a, b), если m = 20; s = 5; a = 15; b = 25. (0,6826).

3. Автомат штампует детали. Контролируется длина детали Х, которая распределена нормально с математическим ожиданием (проектная длина), равным 50 мм. Фактически длина изготовленных деталей не менее 32 и не более 68 мм. Найти вероятность того, что длина наудачу взятой детали:

а) больше 55 мм. (0,0823);

б) меньше 40 мм. (0,0027).

4. Случайные ошибки измерения подчинены нормальному закону со средним квадратическим отклонением s = 20 мм и математическим ожиданием m = 0. Найти вероятность того, что из трех независимых измерений ошибка хотя бы одного не превзойдет по абсолютной величине 4 мм. (0,41).

5. Автомат изготовляет шарики. Шарик считается годным, если отклонение Х диаметра шарика от проектного размера по абсолютной величине меньше 0,7 мм. Считая, что случайная величина Х распределена нормально со средним квадратическим отклонением s = 0,4 мм, найти, сколько в среднем будет годных шариков среди ста изготовленных. (92).

Дата добавления: 2015-06-25