Демонстрационные примеры. Пример 1. Два предприятия А и В изготовляют кирпичную футеровку для кислородных конвертеров

Пример 1. Два предприятия А и В изготовляют кирпичную футеровку для кислородных конвертеров. Потребителю хотелось бы знать, совпадают ли распределения частот плавок, которые можно произвести в конвертере до того, как создается необходимость в замене футеровки, изготовленной на каждом из предприятий. Предполагается, что различия проявляются в несовпадении математических ожиданий, а не в форме распределения, относительно которого нет никаких сведений. Числа плавок до замены футеровки приведены в таблице 13.

Таблица 13

Предприятие	Количество плавок
А										–
В

Решение. Необходимо проверить гипотезу о равенстве математических ожиданий двух совокупностей с неизвестными, но одинаковыми законами распределения Н ₀: М (Х) = М (У) при конкурирующей гипотезе Н ₁: М (Х) ≠ М (У),двусторонней критической областии уровне значимости a = 0,05.

Сначала рассмотрим критерий серий или Вальда-Вольфовица. Запишем для этого все 19 количеств плавок в порядке убывания и подчеркнем те из них, которые относятся к предприятию А:

237, 234, 230, 227, 226, 225, 224, 222, 219, 218, 216, 215, 214, 207, 205, 204, 202, 200, 198.

Полученная последовательность содержит восемь серий значений, относящихся к одному предприятию. Поэтому наблюдаемое значение критерия t_набл = 8. Критическое значение определяется в случае двусторонней критической области, а числа степеней свободы n ₁ = 9, n ₂ = 10 выбираются так, чтобы n ₁ ≤ n ₂. По таблице границ значимости для критерия Вальда-Вольфовица (приложение Е), согласно уровню значимости a = 0,05 и числам степеней свободы n ₁ = 9, n ₂ = 10 находим критические области t ≤ 5 и 15 ≤ t. Так как t_набл не принадлежит ни одному из этих отрезков, то количества плавок отличаются незначимо на уровне a и нет оснований отклонить гипотезу о совпадении математических ожиданий.

Пример 2. рассмотрим гипотезу из примера 1 с помощью медианного критерия. Вычислим медиану совокупности всех количеств плавок. Это можно сделать путем отсчета (n ₁ + n ₂ +1)/2 = 10-го члена последовательности количеств плавок, равного 218. Количества плавок, большие и меньшие чем медиана, обозначим + и –. Тогда последовательность чисел из таблицы 10 примет вид: + + 0 + + – + + + – – – – – – + – + –. Полученная последовательность содержит восемь серий знаков t_набл = 8. В соответствии с той же таблицей (пример 1) приходим к такому же выводу.

Пример 3. Проверим гипотезу из примера 1 с помощью более чувствительных критериев. Обратимся к критерию Вилкоксона и снова рассмотрим последовательность количества плавок, расположенных в порядке убывания. Вычислим сумму порядковых номеров членов этой последовательности, отвечающих предприятию А. Наблюдаемое значение критерия S ₁ = 1 + 2 + 3 + 4 + 6 + 7 + 9 + 10 + 12 = 54. По таблице границ значимости для критерия Вилкоксона (приложение Ж) согласно уровню значимости a = 0,01 и числам степеней свободы n ₁ = 9, n ₂ = 10, которые выбираются так, чтобы n ₁ ≤ n ₂, находим критические области 45 ≤ S ₁≤ 58 и 122 ≤ S ₁ ≤ 135. Так как S ₁ принадлежит левому отрезку, то количества плавок отличаются значимо на уровне a, а гипотеза о совпадении математических ожиданий не согласуется с данными таблицы 13 и поэтому отвергается.

Следует заметить, что право- и левосторонняя критическая область для критерия Вилкоксона имеют одинаковую длину 13, а крайние значения областей 45 и 135 получаются в случаях, когда все данные предприятия А либо меньше, либо больше всех данных предприятия В. В случае a = 0,05 длина этих критических областей увеличивается до 20, а вывод о значимости критерия остается в силе.

Рассмотренный пример показывает, что критерий Вилкоксона является более мощным, чем критерии серий: меньше вероятность принять неверную нулевую гипотезу и совершить ошибку 2-го рода.

С помощью U -критерия Манна-Уитни снова рассмотрим последовательность количества плавок, расположенных в порядке убывания, и вычислим для каждого члена этой последовательности, отвечающего предприятию А, количество членов справа, отвечающих предприятию В. Наблюдаемое значение критерия U = 10 + 10 + 10 + 10 + 9 + 9 + 8 + + 8 + 7 = 81. Это значение связано с критерием Вилкоксона формулой U = n ₁ n ₂ + n ₁(n ₁ + 1)/2 – S ₁ и поэтому приводит к такому же выводу, как критерий Вилкоксона. Следовательно, эти критерии эквивалентны.

Пример 4. рассмотрим гипотезу из примера 1 с помощью критерия Тьюки. Это простой критерий, обладающий очень полезным свойством: границы его критической области почти не зависят от числа степеней свободы. Поэтому критическая область легко запоминается и может быть использована при любых даже очень малых объемах выборок. Важно только чтобы эти объемы отличались не очень сильно.

Обратимся к последовательности количества плавок. Рассмотрим число членов последовательности, относящееся к предприятию А, каждый из которых больше всех членов, относящихся к предприятию В. Полученное число суммируем с аналогичным числом членов, относящихся к предприятию В, каждый из которых меньше всех членов, относящихся к предприятию А. Наблюдаемое значение критерия равно t_набл = 4 + 7 = 11. Критические значения задаются числами

t_кр = 7 при a = 0,05; t_кр = 10 при a = 0,01; t_кр = 13 при a = 0,005.

Таким образом, количества плавок отличаются значимо (t_набл > > t_кр) на уровне a = 0,01, а гипотеза о совпадении математических ожиданий не согласуется с данными таблицы 10 и поэтому отвергается.

Пример 5. группа исследователей выдвинула гипотезу о том, что индивидуумы с ярко выраженными взаимными антипатиями будут чувствовать себя спокойно только тогда, когда они будут находиться на определенном расстоянии друг от друга. Для проверки этой гипотезы провели опрос группы из 35 человек, про напряженные взаимоотношения между которыми было заранее известно. Им было предложено взглянуть на пять фотографий и выбрать из них одну наиболее привлекательную. На фотографиях были изображены два человека, находящиеся на разных расстояниях друг от друга. В таблице 14 приведены частоты n выбора фотографий в зависимости от расстояния между выбирающим лицом и лицами на фотографии в порядке возрастания расстояний, а также относительные частоты n/N.

Таблица 14

Эмпирич. частота	Расстояние	N
n
n/N	3/35	4/35	8/35	11/35	9/35

Необходимо проверить гипотезу о равенстве всех частот Н ₀: n ₁ = = n ₂ = n ₃ = n ₄ = n ₅ = 7 при конкурирующей гипотезе Н ₁: n ₁ ≠ n ₂ ≠ n ₃ ≠ ≠ n ₄ ≠ n ₅ ≠ 7,двусторонней критической областии уровне значимости a = 0,01.

Решение. Применяется критерий Колмогорова-Смирнова. Рассмотрим эмпирическую и теоретическую кумуляту распределения путем суммирования относительных частот, а также максимальное отклонение кумулят. Результаты расчета приведены в таблице 15.

Таблица 15

Кумулята распределения	Расстояние
Fэмп	3/35	7/35	15/35	26/35	35/35
Fтеор	7/35	14/35	21/35	28/35	35/35
Fтеор – Fэмп	4/35	7/35	6/35	2/35

Наблюдаемое значение критерия Колмогорова-Смирнова

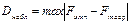= 0,2; критическое значение определяется по таблице точек распределения Колмогорова-Смирнова (приложение И) в зависимости от объема выборки N = 35 и уровня значимости a = 0,01 D_кр (35; 0,01) = 0,27. Так как D_набл < D_кр, то эмпирические и теоретические частоты отличаются незначимо при заданном уровне значимости.

Задания для самостоятельного решения

1. Контролеры, проверяющие качество продукции, производят отбраковку изделий у движущегося конвейера. Двенадцать контролеров пользуются двумя методами отбраковки. Процент отбракованных контролерами изделий при каждом методе приведен в таблице 16.

Таблица 16

Метод 1

Метод 2

Используя критерий Тьюки проверить при уровне значимости a = = 0,01 эквивалентность методов (t ≤ 10; t_набл = 12).

2. При 20 бросаниях монеты получена последовательность выпадений герба (Г) и цифры (Ц): Г Г Г Ц Г Ц Ц Ц Ц Г Г Г Ц Ц Г Г Ц Ц Г Г. Используя критерий Вальда-Вольфовица, решить при уровне значимости a = 0,05, есть ли основания считать, что эта последовательность получена не случайным образом (t ≤ 6 и t ³ 15; t_набл = 9).

3. Средний объем стока воды в реке фиксируется каждый месяц в течение двух лет. В таблице 17 приведены объемы стока в фут³/сек.

Таблица 17

Год

янв

фев

март

апр

май

июн

июл

авг

сен

окт

ноя

дек

Используя критерий Вилкоксона, проверить при уровне значимости a = 0,01 гипотезу об отсутствии систематического изменения объема стока из года в год (S ₁ ≤ 105 и S ₁ ³ 195; S_набл = 153).

4. Используя критерий Колмогорова-Смирнова для данных таблицы 18, проверить гипотезу о равномерном распределении частот при уровне значимости a = 0,05 (D_набл = 0,133 < D_кр = 0,24).

Таблица 18

Эмпирич. частота	Порядковая позиция	N
n

Дата добавления: 2015-06-25