Демонстрационные примеры. Вопросы для теоретической подготовки

Вопросы для теоретической подготовки

Тема 10. Элементы теории статистических гипотез

Ø Цель: познакомить с типами статистических гипотез и критериями их проверки.

1. Основная и альтернативная гипотеза. Статистический критерий и его критическая область. Виды критических областей.

2. Ошибки 1-го и 2-го рода. Уровень значимости и мощность критерия.

3. Критерий согласия Пирсона проверки гипотезы о нормальном законе распределения генеральной совокупности.

4. Критерий Фишера-Снедекора проверки гипотезы о совпадении двух дисперсий нормальных генеральных совокупностей. Условия применения критерия.

5. Критерий Стьюдента проверки гипотезы о совпадении двух математических ожиданий нормальных генеральных совокупностей в случае известных и неизвестных, но равных дисперсий.

6. Критерий согласия Пирсона проверки гипотезы о независимости двух признаков с помощью таблицы сопряженности признаков.

7. Критерий Стьюдента проверки гипотезы об отсутствии корреляционной зависимости между двумя нормальными генеральными совокупностями.

Пример 1. Используя критерий согласия Пирсона c ² при уровне значимости 0,05, проверить, согласуется ли гипотеза о нормальном распределении случайной величины с заданным распределением выборки из примера 1, рассмотренного в теме 5.

Решение. Используя метод произведений, найдем выборочные среднюю 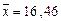(см. пример 2, тема 8) и исправленное среднее квадратическое отклонение 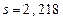(см. пример 3, тема 8). Вычислим теоретические частоты, учитывая, что n = 100, h = 2, s = 2,218, по формуле

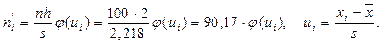
Составим расчетную таблицу 6 значений эмпирических n_i и теоретических n_i ^¢ частот, в которой значения функции j (u_i) помещены в приложении А

Таблица 6

номер i							S
варианта хi
частота ni
ui	–2,01	–1,11	–0,21	0,694	1,596	2,498
j (ui)	0,053	0,215	0,39	0,313	0,098	0,018
ni ^¢	4,78	19,39	35,17	28,22	8,84	1,62
ni – ni ^¢	0,22	–4,39	14,83	–12,2	1,16	2,38
(ni – ni ^¢)^2	0,048	19,27			1,35	5,66
(ni – ni ^¢)^2/ ni ^¢	0,01	0,99	6,26	5,28	0,15	3,49	16,18

Из таблицы 6 находим наблюдаемое значение критерия согласия Пирсона 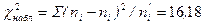, которое характеризует степень отличия теоретических и эмпирических частот. По таблице критических точек распределения c ² (приложение В), согласно уровню значимости a = 0,05 и числу степеней свободы k = 6 – 3 = 3 (6 – максимальный номер i) находим критическую точку 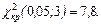Так как 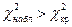, то теоретические и эмпирические частоты отличаются значимо на уровне a, а гипотеза о нормальном распределении случайной величины не согласуется с заданным распределением выборки.

Пример 2. В результате обработки двух независимых выборок, объемы которых соответственно равны n_x = 5 и n_у = 6, извлеченных из нормальных генеральных совокупностей Х и У, найдены выборочные исправленные дисперсии 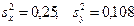(см. примеры 2 и 3, тема 8). Используя критерий Фишера-Снедекора проверить гипотезу о равенстве дисперсий двух нормальных совокупностей Н ₀: D (Х) = D (У) при конкурирующей гипотезе Н ₁: D (Х) > D (У) и уровне значимости

a = 0,05.

Следует отметить, что в качестве совокупности Х выбирается та, для которой исправленная дисперсия больше.

Решение. Используя критерий Фишера-Снедекора, вычислим наблюдаемое значение критерия по формуле F_набл = 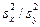= 2,31. По таблице критических точек распределения Фишера-Снедекора (приложение Д), согласно уровню значимости a = 0,05 и числам степеней свободы k ₁ = 5 – 1 = 4, k ₂ = 6 – 1 = 5 находим критическую точку распределения F_кр = 5,19. Так как 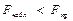, то выборочные исправленные дисперсии отличаются незначимо на уровне значимости a и нет оснований отвергнуть гипотезу о равенстве дисперсий двух нормальных генеральных совокупностей.

Пример 3. Используя критерий Стьюдента проверить гипотезу о равенстве математических ожиданий двух нормальных совокупностей с неизвестными, но равными дисперсиями Н ₀: М (Х) = М (У) при конкурирующей гипотезе Н ₁: М (Х) ≠ М (У) и уровне значимости a = 0,05.

В результате обработки двух независимых выборок, объемы которых соответственно равны n_x = 5 и n_у = 6, извлеченных из нормальных генеральных совокупностей Х и У, найдены выборочные средние и исправленные дисперсии 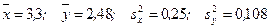(см. пример 2).

Решение. Используя критерий Стьюдента, вычислим наблюдаемое значение критерия по формуле

.

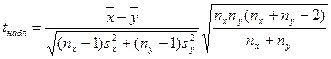Подставляя заданные значения в эту формулу получим t_набл = 3,27. Критическое значение определяется в случае двусторонней критической области, а число степеней свободы k = 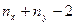. По таблице критических точек распределения Стьюдента (приложение Г), согласно уровню значимости a = 0,05 и числу степеней свободы k = 5 + 6 – 2 = 9 находим критическую точку t_кр = 2,26. Так как 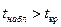, то выборочные средние отличаются значимо на уровне a, а гипотеза о равенстве математических ожиданий двух нормальных совокупностей не согласуется с заданными распределениями выборок.

Пример 4. Используя критерий согласия Пирсона c ² при уровне значимости 0,05 проверить, согласуется ли гипотеза о независимости уровня успеваемости от фамилии студента с результатами успеваемости двух студентов разных курсов. Результаты успеваемости студентов приведены в таблице 7 сопряженности рассматриваемых признаков, где указаны частоты полученных оценок за период обучения.

Таблица 7 – Эмпирические частоты оценок

Фамилия	Оценки студентов	Всего
Иванов
Петров
Итого

Решение. Введем следующие обозначения: i – номер строки таблицы, который равен 1, 2; j – номер столбца, который равен 1, 2, 3, 4; N_ij – эмпирическая частота, расположенная на пересечении i -й строки и j -го столбца. Для оценивания доли количества оценок каждого студента используются отношения N_i./N, где 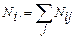, 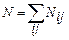= 110. Аналогично доли всех “пятерок”, “четверок” и так далее оцениваются отношениями N._j /N, где . Если уровни успеваемости студентов отличаются незначимо, то приведенные в таблице 4 частоты приближаются теоретическими частотами 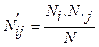. Составим таблицу 8 теоретических частот.

Таблица 8 – Теоретические частоты оценок

Фамилия	Оценки студентов	Всего
Иванов	24,55	19,09	5,91	0,45
Петров	29,45	22,91	7,09	0,55
Итого

Наблюдаемое значение критерия с учетом теоретических частот 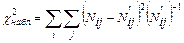= 16,18, которое характеризует степень отличия теоретических и эмпирических частот. По таблице критических точек распределения c ² (приложение В), согласно уровню значимости a = 0,05 и числу степеней свободы k = (4 – 1)(2 – 1) = 3 (4 – максимальный номер j, 2 – максимальный номер i) находим критическую точку 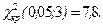Так как 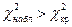, то теоретические и эмпирические частоты отличаются значимо на уровне a, а гипотеза о независимости уровней успеваемости студентов не согласуется с данными успеваемости.

Пример 5. В результате обработки двумерной выборки объема n = = 100, извлеченной из нормальной генеральной совокупности (Х,У), методом произведений (см. пример, тема 9) найден выборочный коэффициент корреляции r_в = 0,76.

Используя критерий Стьюдента, проверить гипотезу об отсутствии корреляционной зависимости между двумя нормальными генеральными совокупностями Н ₀: r_ху = 0 при конкурирующей гипотезе

Н ₁: r_ху ≠ 0 и уровне значимости a = 0,05.

Решение. Используя критерий Стьюдента, вычислим наблюдаемое значение критерия по формуле 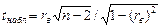= 11,58. Критическое значение определяется в случае двусторонней критической области, а число степеней свободы k = 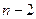. По таблице критических точек распределения Стьюдента (приложение Г), согласно уровню значимости a = 0,05 и числу степеней свободы k = 100 – 2 = 98 находим критическую точку t_кр = 1,985. Так как 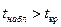, то выборочный коэффициент корреляции отличаются от нуля значимо на уровне a, а гипотеза о об отсутствии корреляционной зависимости между двумя переменными Х,У не согласуется с данными выборки.

Задания для самостоятельного решения

1. В результате обработки выборки из генеральной совокупности получены следующие частоты вариант (таблица 9).

Таблица 9 – Эмпирические и теоретические частоты

Эмпирические
Теоретические

При уровне значимости 0,05 проверить, согласуется ли гипотеза о нормальном распределении случайной величины с заданным распределением выборки (c ² _набл = 7,19 < c ² _кр (0,05; 5) = 11,1).

2. В результате обработки двух независимых выборок, объемы которых n_x = n_у = 10, извлеченных из нормальных генеральных совокупностей Х и У, найдены выборочные средние и исправленные дисперсии 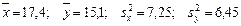. Используя критерий Стьюдента, проверить гипотезу о равенстве математических ожиданий двух нормальных совокупностей с неизвестными, но равными дисперсиями Н ₀: М (Х) = М (У) при конкурирующей гипотезе Н ₁: М (Х) ≠ М (У) и уровне значимости 0,05 ().

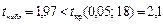3. Анализ ранних произведений Эрнеста Хемингуэя показал, что предложения, включающие разное число слов, распределены в них следующим образом (таблица 10).

Таблица 10 – Относительные частоты предложений

Число слов	2-3	4-5	6-8	9-12	13-16	17-20	21-24	25-28	> 28
Частота	0,01	0,034	0,067	0,091	0,21	0,174	0,181	0,143	0,09

Наследники автора заявили о находке рукописи ранее неопубликованного произведения своего предка. В выборке, состоящей из 2000 предложений, было обнаружено следующее распределение фраз по длине (таблица 11).

Таблица 11 – Частоты предложений

Число слов	2-3	4-5	6-8	9-12	13-16	17-20	21-24	25-28	> 28
Частота

Могут ли эти данные подтвердить заявление наследников? (c ² _набл = = 61,4, что больше критического значения при любом a).

4. Используя критерий согласия Пирсона c ² при уровне значимости 0,05, проверить, согласуется ли гипотеза о независимости уровня успеваемости от фамилии студента с результатами успеваемости трех студентов разных курсов. Результаты успеваемости студентов приведены в таблице сопряженности рассматриваемых признаков, где указаны частоты полученных оценок за период обучения (c ² _набл = 8,92 < < c ² _кр (0,05; 6) = 12,53).

Таблица 12 – Эмпирические частоты оценок

Фамилия	Оценки студентов	Всего
Иванов
Петров
Сидоров
Итого

5. Используя критерий Стьюдента для проверки гипотезы об отсутствии корреляционной зависимости между двумя нормальными генеральными совокупностями Н ₀: r_ху = 0 при конкурирующей гипотезе Н ₁: r_ху ≠ 0 и уровне значимости a = 0,05, найти критическое значение выборочного коэффициента корреляции для выборки объема n = 100 (0,196).

Дата добавления: 2015-06-25