Демонстрационные примеры. Вопросы для теоретической подготовки

Вопросы для теоретической подготовки

Тема 6. Числовые характеристики дискретной

случайной величины (дсв)

Ø Цель: научить вычислять числовые характеристики дсв и вероятность попадания дсв в заданный интервал.

1. Математическое ожидание дсв, его вероятностный и механический смысл.

2. Свойства математического ожидания. Математическое ожидание биномиального и пуассоновского распределения.

3. Дисперсия, ее вероятностный и механический смысл.

4. Свойства дисперсии. Дисперсия биномиального и пуассоновского распределения.

5. Среднее квадратическое отклонение и его свойства.

6. Числовые характеристики геометрического распределения.

7. Локальная и интегральная теоремы Лапласа.

Пример 1. Дискретная случайная величина Х имеет только два возможных значения: х ₂ > х ₁. Вероятность того, что Х примет значение х ₁, равна 0,6. Найти закон распределения величины Х, если математическое ожидание и дисперсия известны: М (Х) = 1,4; D (Х) = 0,24.

Решение. Сумма вероятностей всех возможных значений дискретной случайной величины равна единице, поэтому вероятность того, что Х примет значение х ₂, равна 0,4. Для отыскания х ₁ и х ₂ надо составить два уравнения, связывающие эти числа. С этой целью выразим известные математическое ожидание и дисперсию через х ₁ и х ₂. Математическое ожидание М (Х) = 0,6 х ₁ + 0,4 х ₂. По условию, М (Х) = 1,4, следовательно,

0,6 х ₁ + 0,4 х ₂ = 1,4.

Одно уравнение, связывающее х ₁ и х ₂, получено. Для того, чтобы получить второе уравнение, выразим известную дисперсию через х ₁ и х ₂. Найдем М (Х ²) = 0,6(х ₁)² + 0,4(х ₂)². Найдем дисперсию D (X) = M (X ²)– – [ M (X)]² = 0,6(х ₁)² + 0,4(х ₂)² – (1,4)². Подставляя D (Х) = 0,24, после элементарных преобразований получим

0,6 (х ₁)² + 0,4 (х ₂)² = 2,2.

Решив систему двух полученных уравнений, найдем два решения:

х ₁ = 1; х ₂ = 2 и х ₁ = 1,8; х ₂ = 0,8.

По условию х ₂ > х ₁, поэтому задаче удовлетворяет только первое решение: х ₁ = 1; х ₂ = 2. Получается следующий закон распределения:

Х
р	0,6	0,4

Пример 2. Вероятность попадания в мишень при одном выстреле равна 0,6. Найдите закон распределения вероятностей случайного числа попаданий в мишень при пяти выстрелах, математическое ожидание, дисперсию и среднее квадратическое отклонение этого распределения.

Решение. По условию, случайная величина имеет биномиальный закон распределения с параметрами n = 5; р = 0,6; q = 0,4:

Р ₅(к) = С₅ ^к (0,6)^к (0,4)^{5– к} , к = 0, …, 5.

Получается следующий закон распределения:

к
Р 5(к)	0,01024	0,0768	0,2304	0,3456	0,2592	0,07776

Математическое ожидание биномиального распределения вычисляется по формуле М(Х) = np = 5×0,6 = 3. Дисперсия биномиального распределения вычисляется по формуле D(Х) = npq = 5×0,6×0,4 = 1,2. Среднее квадратическое отклонение s(Х) = 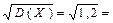1,095.

Пример 3. Вероятность поражения мишени при одном выстреле равна 0,6. Какова вероятность того, что при 2400 выстрелах мишень будет поражена ровно 1400 раз?

Решение. По условию, n = 2400; k = 1400; р = 0,6; q = 0,4. Так как n велико, воспользуемся локальной теоремой Лапласа:

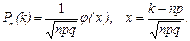
Найдем значение х = (1400 – 2400×0,6)/24 = –1,67. Функция j (х) – четная, поэтому j (–1,67) = j (1,67). По таблице приложения А найдем j (1,67) = 0,0989. Искомая вероятность

Р ₂₄₀₀(1400) = 1/24×0,0989 = 0,0041.

Пример 4. Вероятность поражения мишени при одном выстреле равна 0,8. Какова вероятность того, что при 100 выстрелах мишень будет поражена:

а) не менее 75 раз и не более 90 раз;

б) не менее 75 раз;

в) не более 74 раз?

Решение. Воспользуемся интегральной теоремой Лапласа:

P_n (k ₁, k ₂) = F (x ¢¢) – F (x ¢),

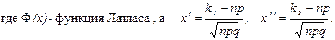
а) По условию, n = 100; k ₁ = 75; k ₂ = 90; р = 0,8; q = 0,2. Вычислим x ¢ = –1,25; x ¢¢ = 2,5. Учитывая, что функция Лапласа нечетная, то есть F (– x) = – F (x), получим P ₁₀₀(75, 90) = F (2,5) – F (–1,25). По таблице приложения Б найдем: F (2,5) = 0,4938; F (1,25) = 0,3944. Искомая вероятность P ₁₀₀(75, 90) = 0,8882.

б) Требование, чтобы событие появилось не менее 75 раз, означает, что число появлений события может быть равно 75 либо 76, …, либо 100. Таким образом, в рассматриваемом случае следует принять k ₁ = 75; k ₂ = 100. Тогда x ¢ = –1,25; x ¢¢ = 5. По таблице приложения 2 найдем: F (5) = 0,5; F (1,25) = 0,3944. Искомая вероятность P ₁₀₀(75, 100) = = 0,8944.

в) События – «мишень будет поражена не менее 75 раз» и «мишень будет поражена не более 74 раз» противоположны, поэтому сумма вероятностей этих событий равна единице. Следовательно, искомая вероятность P ₁₀₀(0, 74) = 1 – 0,8944 = 0,1056.

Задания для самостоятельного решения

1. Дискретная случайная величина Х может принимать только два значения: х ₂ > х ₁. Вероятность того, что Х примет значение х ₁, равна 0,1. Найти закон распределения величины Х, если математическое ожидание и дисперсия известны: М(Х) = 3,9; D(Х) = 0,09. (3; 4).

2. Найти вероятность того, что из 400 банков сохранится только 80, если вероятность выживаемости каждого банка равна 0,2. (0,0498).

3. Найти вероятность того, что из 500 посеянных семян не взойдет 130, если вероятность всхожести семян 0,75. (0,036).

4. Найти вероятность того, что из 400 банков сохранится от 70 до 100 банков, если вероятность выживаемости каждого банка равна 0,2. (0,8882).

5. Вероятность поражения мишени стрелком при одном выстреле равна 0,75. Найти вероятность того, что при 100 выстрелах мишень будет поражена:

а) не менее 70 и не более 80 раз. (0,7498);

б) не более 70 раз. (0,1251).

Дата добавления: 2015-06-25