Демонстрационный пример

Вопросы для теоретической подготовки

Тема 9. Элементы теории корреляции

Ø Цель: научить устанавливать корреляционную зависимость между двумя нормальными случайными величинами.

1. Какая зависимость называется корреляционной и чем она отличается от функциональной?

2. Компоненты двумерной случайной величины и их числовые характеристики: условные плотность и математическое ожидание.

3. Корреляционный момент и коэффициент корреляции, их вероятностный смысл и свойства.

4. Выборочное уравнение прямой линии регрессии и его числовые характеристики.

5. Выборочное уравнение нелинейной регрессии. Метод выравнивания зависимости.

Найти выборочное уравнение прямой линии регрессии Y на X согласно протоколу наблюдений двумерной выборки (х_i,у_i), i = 1, …,100, приведенному в таблице 3.

Таблица 3

Х	У	Х	У	Х	У	Х	У	Х	У
21,47							23,93		48,01
	45,48	24,14		28,64	46,61	34,03	36,02		26,91
24,23		19,85	18,02		23,01	23,74	17,85	29,24	43,37
	53,39	18,53	19,46	30,07	43,17	28,5	36,29	36,81	45,36
	46,96		41,89	32,4	37,49	31,17		35,28	57,47
	27,11	29,95			55,72	29,95	38,19
24,13		28,45		35,18	40,14		28,62	23,83	15,5
	31,25		32,38		49,12	30,66			24,51
	35,26		31,64		36,74
	25,3			28,5	32,09	30,25			35,33
	34,94		57,79	29,8	33,71			35,47
29,5	31,62	30,97				19,52	18,32
36,09						26,49	23,73	38,5	42,65
31,13	27,67		38,74	28,84		39,5		35,89
32,06	22,49	34,9	44,15		45,67			33,71	45,63
	32,91			27,5	39,26	30,33	38,59
31,84		32,19	39,54	40,36	33,36	30,43	28,75	40,5	40,32
	39,56	34,19	35,6		36,47			33,18	43,88
30,5	38,23	36,38	44,08	30,5	39,66	22,73	20,05
	29,35	28,58	30,05	35,59	47,63	36,21	47,95

Решение. Наблюдения двумерной выборки в виде 100 точек с координатами (х_i,у_i) изображаются на координатной плоскости и заключаются в прямоугольник, который разбивается на прямоугольные клетки со сторонами h_x и h_y подобно тому, как разбивается отрезок на k интервалов в примере 1 темы 8. На рисунке 6 выбрано k = 5, а шаги h_x = = 5, h_y = 10.

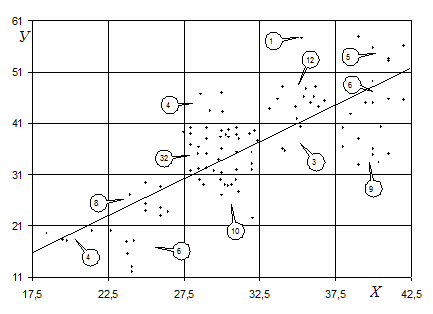
Рисунок 6 – Группировка наблюдений двумерной выборки

Количество точек, попавших в клетку, отмечено в выносках и рассматривается как частота n_ху центра соответствующей клетки. Если точка расположена на границе, разделяющей две клетки, то она относится к той клетке, в которой находится больше точек. Найденные таким образом значения частот приведены в клетках корреляционной таблицы 4, обведенных двойной линией. Сверху и слева указаны соответствующие координаты центра клетки (варианты Х, У), а снизу и справа – суммарные частоты вариант.

Таблица 4

У	X	ny
			-	-	-
	-			-	-
	-	-
	-	-
	-	-	-
nx						n = 100

Для каждой случайной величины X и У вводятся условные варианты u и v подобно тому, как это делается в примере 2, рассмотренном в теме 8. Составим корреляционную таблицу 5 в условных вариантах

Таблица 5

v	u	nv	U=Snuvu	vU
–2	–1
–2	–8	–6					–14
–1		–8					–8
nu							S vU = 82

Методом произведений (см. таблицу 2) найдем выборочные средние:

Выборочные средние квадратические отклонения условных вариант u и v найдем по формулам:

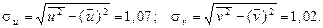
Затем проверяется гипотеза о нормальном распределении генеральных совокупностей X и У (см. пример 1, тема 10). Только после этого отыскивается выборочный коэффициент корреляции.

Произведение частоты n_uv на варианту u, то есть n_uvu, записывают в правом верхнем углу клетки таблицы 5, содержащей частоту n_uv. Например, в правых верхних углах клеток первой строки записаны произведения: 4(–2) = –8; 6(–1) = –6. В предпоследнем столбце приведены значения U=Sn_uvu, которые получаются суммированием по строкам чисел в правых верхних углах. В последнем столбце приведены произведения числа U и соответствующего числа v. Суммируя числа последнего столбца найдем Sn_uvuv = S vU = 82.

Выборочный коэффициент корреляции найдем по формуле

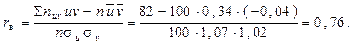
Поскольку значение r_в > 0,196, то с уровнем значимости 0,05 можно утверждать о зависимости У от Х. Если это условие не выполняется, то можно принять гипотезу об отсутствии корреляционной зависимости с отмеченным уровнем значимости (см. задачу 5, тема 10).

Найдем выборочные средние 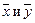, учитывая, что шаги h_x = 5, h_y = = 10, а ложные нули С_х = 30; С_y = 36:

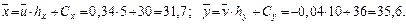
Затем найдем выборочные средние квадратические отклонения:

s _x = h_x s _u = 5 ×1,07 = 5,35; s _y = h_y s _v = 10 ×1,02 = 10,2.

Подставим найденные величины в уравнение регрессии Y на X

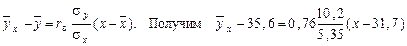
или окончательно График полученной корреляционной зависимости приведен на рисунке 6. Этот график разбивает облако данных на две симметричные части и наилучшим образом приближает эти данные.

Дата добавления: 2015-06-25