Статика. Под фермой понимают жесткую неизменяемую конструкцию, состоящую из стержней и соединяющих их шарниров

Статика

Под фермой понимают жесткую неизменяемую конструкцию, состоящую из стержней и соединяющих их шарниров. Отметим, что любая реальная ферма и ее расчетная схема - это, как говорят юмористы, две большие разницы. Ферма может быть деревянной, металлической или железобетонной, а на расчетной схеме выглядеть паутинкой тонких линий и при весе в несколько тонн считаться состоящей из как бы невесомых стержней. Связано это с весьма сильными допущениями, которые применяются при расчетах ферм и о которых просто необходимо знать. Допущения эти следующие:

1) стержни фермы считаются невесомыми;

2) шарниры, соединяющие стержни между собой, считаются идеальными, то есть без трения;

3) силы, действующие на фермы, считаются приложенными только в узлах фермы - то есть в связывающих стержни шарнирах.

(Таким образом учитывают и силы тяжести стержней. Эти силы просто делят между узлами.)

Перечисленные выше допущения позволяют приближенно считать, что на каждый из узлов фермы действует только сходящаяся система сили, следовательно, стержни фермы либо растянуты, либо сжаты. Результаты расчетов при таких допущениях, конечно, весьма приближенные. Но на практике эту неточность расчетов считают допустимой. Абсолютно точно рассчитать усилия в стержнях практически невозможно.

Конструкций ферм существует довольно много. Разнообразные классификации ферм (по материалу, по назначению, по конструкции и так далее) рассматриваются в специальных дисциплинах. А на практических занятиях по "СТАТИКЕ" студенты учатся определять усилия в стержнях любых плоских ферм (оси стержней которых расположены в одной плоскости) и... проверять результаты своих расчетов.

Фермой называется жесткая (кинематически неизменяемая) конструкция, состоящая из прямолинейных стержней, соединенных на концах шарнирами. Места соединения стержней называются узлами, к которым прикладываются внешние силы. Весом стержней и трением в шарнирах пренебрегают. В случае необходимости учета их веса, вес стержней распределяют по узлам. Следовательно, на каждый стержень фермы действуют только две силы, приложенные по его концам. Поэтому стержни работают либо на растяжение, либо на сжатие. Таким образом, на каждый узел действует система сходящихся сил. Если стержни расположены в одной плоскости, то такая ферма называется плоской.
В плоской ферме различают следующие элементы: верхний пояс, нижний пояс, стойки, раскосы, узлы, панели (рис. 4.1).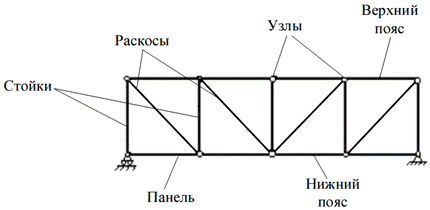
Рис. 4.1

Стержни, располагающиеся на верхнем контуре фермы, образуют верхний пояс, а находящиеся на нижнем контуре – нижний пояс. Стержни, соединяющие узлы панели, образуют решётку фермы, при этом наклонные стержни называются раскосами, а вертикальные стержни – стойками. Часть фермы, находящаяся между узлами поясов, называется панелью.
В инженерной практике стержни обычно жёстко соединены в узлах с помощью сварных, заклёпочных или болтовых соединений, при этом в жёстких узлах возникают изгибающие моменты. Однако, напряжения изгиба по сравнению с нормальным напряжением весьма малы, поэтому ими, при расчёте фермы, как правило, пренебрегают.
Фермы используются при устройстве мостовых переходов, перекрытий большепролётных зданий, создании грузоподъёмных устройств (например, строительных кранов).
Большое разнообразие конструктивных решений ферм затрудняет их классификацию. В настоящее время фермы классифицируют по следующим признакам:
1) по характеру усилий – фермы балочные (рис. 4.2а), висячие (рис. 4.2б), комбинированные (рис. 4.2в);

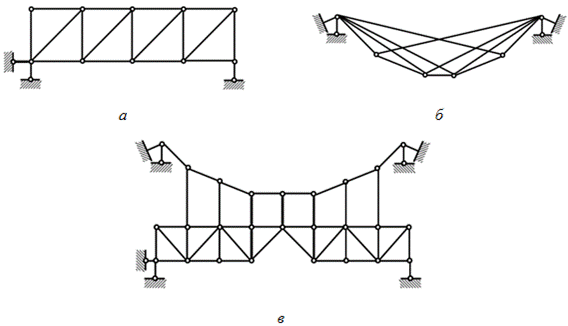
Рис. 4.2

2) по очертанию поясов фермы – с параллельными поясами (рис. 4.2а), с полигональными поясами (рис. 4.3б), треугольными поясами (рис. 4.3в);

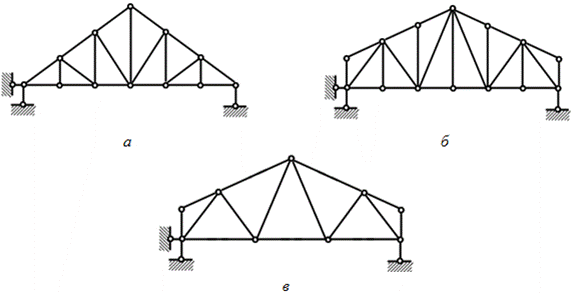
Рис. 4.3

1) по конфигурации решетки – раскосные (рис. 4.2а), с треугольной решеткой (рис. 4.4а), полураскосные (рис. 4.4б), многораскосные (рис. 4.4в), решетчатые (рис. 4.4г).

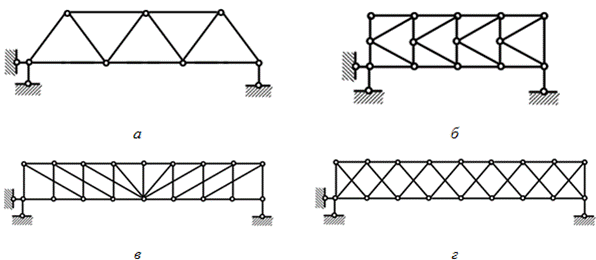
Рис. 4.4

Фермы с составной решёткой называются шпренгельными фермами. Шпренгелями называют дополнительные малые фермочки, которые можно рассматривать как элементы верхнего или нижнего поясов фермы (рис. 4.5).

Рис. 4.5

Определение «нулевых» стержней производится согласно леммах о «нулевых» стержнях.
Лемма I. Если в ненагруженном узле плоской фермы сходятся два стержня, то усилия в этих стержнях равны нулю (рис. 4.7а).

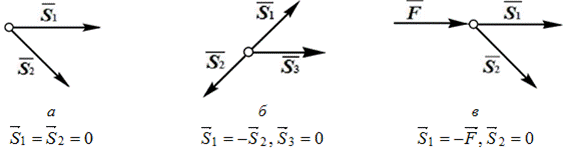
Рис. 4.7. «Нулевые» стержни фермы

Лемма II. Если в ненагруженном узле плоской фермы сходятся три стержня, из которых два расположены на одной прямой, то усилие в третьем стержне равно нулю, а усилия в первых двух стержнях равны между собой (рис. 4.7б).
Лемма III. Если в узле плоской фермы сходятся два стержня и к узлу приложена сила, линия действия которой совпадает с осью одного из стержней, то усилие в этом стержне по модулю равно приложенной силе, а усилие в другом стержне равно нулю.
Расчет плоских ферм заключается в определении реакций внешних связей (опорных узлов) и усилий в стержнях.

Дата добавления: 2015-06-04