К простейшему виду

НЕ НАХОДЯЩЕЙСЯ В РАВНОВЕСИИ,

ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ,

СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ

ПРИВЕДЕНИЕ ПРОИЗВОЛЬНОЙ

(ПЛОСКОЙ ИЛИ ПРОСТРАНСТВЕННОЙ)

В этом случае система сил 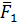, , 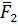, 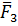…, 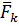заменяется одной силой 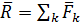и суммой моментов, а именно произведений каждой из этих сил на расстояние от точки её приложения до некоторого центра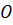

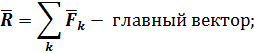
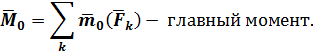
Замечания.

1. Сила 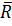не является здесь равнодействующей, так как заменяет систему сил не одна, а с появившейся парой сил, имеющей момент .

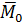2. Значение 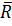от выбора центра 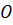не зависит, а значение 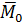меняется с изменением центра 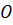, в который переносятся силы.

Результат приведения зависит от значений и направлений главного вектора 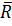и главного момента .

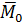Случай 1: .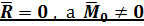

Система сил приводится к паре сил с моментом 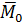. Значение 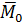от выбора центра 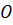не зависит. Это значение вычисляется по составляющим его проекциям

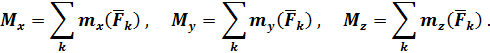
Случай 2: .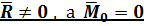

Система сил приводится к равнодействующей 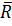, приложенной в центре 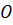. Значение 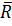вычисляется по составляющим её проекциям

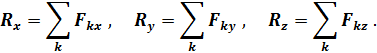
Случай 3: .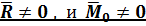

Система сил приводится к равнодействующей 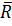, но (!) не приложенной в центре .

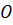В этом случае может быть три варианта (3.1, 3.2 и 3.3).

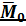Вариант 3.1: , причём перпендикулярен .

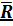Система сил приводится к силе 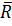и паре сил 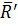и 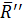, лежащих в той же плоскости, что и 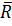, и создающих момент 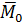(рис. 26).

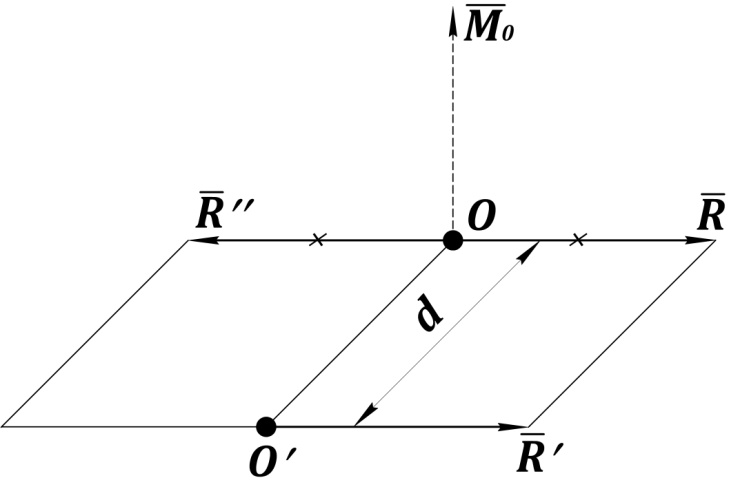
Рис. 26. Приведение пространственной системы сил

к простейшему виду:

, причём 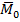перпендикулярен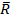

Можно принять 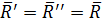. Тогда силы уравновесятся ().

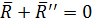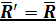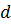Система сил приводится к одной равнодействующей , приложенной в точке . Расстояние от точки 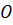до точки определяется из выражения

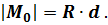
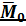Вариант 3.2: , причём параллелен .

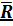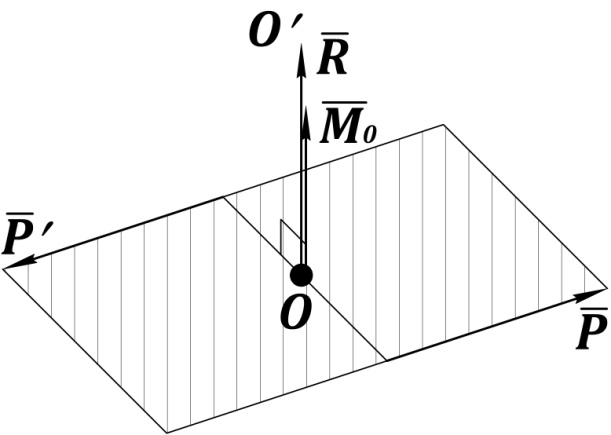
Рис. 27. Приведение пространственной системы сил

к простейшему виду:

, причём 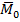параллелен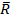

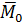– момент от пары сил 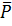и 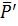(рис. 27).

Совокупность силы 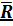и пары сил 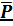и 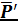называется динамическим винтом с осью 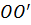по линии действия .

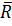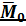Вариант 3.3: , но и 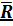не перпендикулярны и не параллельны.

В этом варианте система сил тоже приводится к динамическому винту, но его ось не проходит через центр 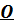(рис. 28).

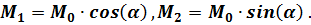
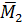перпендикулярен 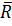, значит может быть замена, как в варианте 3.1:

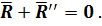
Остаются:

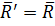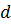¾ сила в точке на расстоянии от точки ;

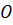¾ момент 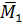, как свободный, перенесённый в точку .

Рис. 28. Приведение пространственной системы сил

к простейшему виду:

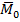, но и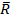

не перпендикулярны и не параллельны

Дата добавления: 2015-06-04