Пример 3.6. Элементы комбинаторики

Пример 3.5

Элементы комбинаторики

Перестановки – это такие комбинации из совокупности 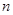различных элементов, которые отличаются только порядком следования элементов. Число перестановок из 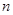элементов 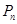вычисляется по формуле

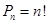
(3.1)

Напомним, что (читается: “ 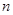факториал”) это произведение чисел от 1 до 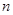): 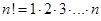, при этом, для удобства записи некоторых формул, принимается, что 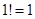и .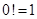

Из цифр 1, 2, 3 можно составить трехзначные числа: 123, 132, 213, 231, 312, 321. Каждая такая комбинация представляет собой перестановку из трех элементов. Число этих перестановок .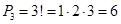

Размещения – это комбинации из 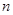различных элементов по m элементов, которые отличаются составом элементов или порядком. Число размещений из 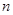элементов по т элементов вычисляется по формуле

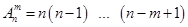
(3.2)

Из цифр 1, 2, 3 можно составить двухзначные числа 12, 21, 13, 31, 23, 32. Каждая такая комбинация представляет собой размещение из трех элементов по два элемента. Число этих размещений .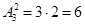

Сочетания – это комбинации из 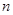по т элементов, которые различаются хотя бы одним элементом. Число сочетаний из 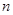элементов по т элементов вычисляется по формуле

,

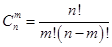(3.3)

причем , .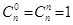

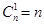Дата добавления: 2015-06-26