Пример 3.13. Пусть, как и в предыдущем примере в ящике 3 крас­ных и 7 белых шаров

Решение

Пример 3.12

Пусть, как и в предыдущем примере в ящике 3 крас­ных и 7 белых шаров. Наугад извлекается 5 шаров. Найдем вероятность того, что 2 из них окажутся красными и 3 – белыми.

Общее число способов, которыми можно из­влечь 5 шаров из 10, равно 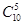. Следовательно общее число исходов испытания равно 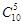. Число способов, которыми из трех красных шаров можно извлечь 2 шара, равно 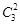. С каждым из этих способов сочетаются все комбинации, которые можно получить, извлекая 3 шара из 7 белых, т. е. 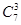. Таким об­разом, число благоприятствующих исходов равно 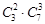. Следовательно, =

= .

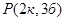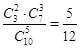(Гипергеометрическое распределение). В ящике содержатся N шаров, среди которых М красных и белых. Наугад извлекаются 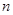шаров. Требуется най­ти вероятность того, что среди них окажется ровно т красных (и 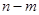белых).

Искомая вероятность находится по формуле:

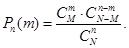
(3.5)

В общем случае рассмотренная задача может быть сформулирована следующим образом. В группе из N предметов имеются М предметов, обладающих некоторым свойством 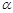, остальные N – М предметов этим свойством не обладают. Из этой группы наугад выбирают­ся 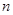предметов. Чему равна вероятность события «в выбор­ке оказалось ровно т предметов, обладающих свойством »?

Формула (3.5) каждому значению 0, 1, 2..., 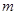(количеству предметов, обладающих свойством ), ставит в соответствие вероятность появления этого количества. Можно сказать, что формула (3.5) определяет распределение вероятностей. Распределение вероятностей, определяемое формулой (3.5), называется гипергеометрическим.

Рассмотренная задача играет большую роль в приложе­ниях: в демографии, статистике населения, статистическом контроле качества промышленной продукции и т. д. При желании с помощью формулы (3.5) можно найти вероят­ность угадывания любого числа из разыгрываемых номеров в спортлото (см. также задание 4 тренировочного теста в конце раздела).

Во всех приведенных примерах применение формулы (3.4) основывалось на предположении о равновозможности исходов испытания. Такое предполо­жение оправдано в случаях симметрий условий: при подбрасывании идеального ку­бика, при извлечении наугад хорошо перемешанных шаров и т. д. Но даже в этих простейших случаях равновозможность исходов является предположением (допущением). Если же такое допущение невозможно (а в реальном мире идеальных кубиков не бывает), то классическое определение оказывается непригодным.

Дата добавления: 2015-06-26