Пример 3.16

Теорема умножения вероятностей

Из равенства (3.6) следует, что

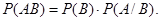
(3.7)

Эта формула называется теоремой умножения вероятно­стей.

Обобщения теоремы умножения на случай трех и большего числа событий соответственно имеют вид

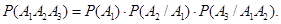
(3.8)

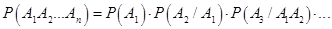
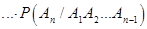
	(3.9)

Из 20 вопросов программы студент вы­учил 16. Требуется найти вероятность того, что 3 предло­женных вопроса окажутся знакомыми (событие ).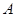

Решение

Обозначим 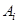- событие « вопрос оказался знакомым» (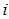 = 1, 2, 3). Тогда . Можно представить, что вопросы записаны на отдельных карточках и выбираются наугад один за другим (без возвращения). Тогда 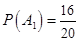, 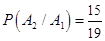(вероятность получения второго знакомого вопроса при условии, что первый оказался знакомым), 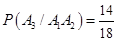(вероятность третьего «везения» при условии, что знакомыми оказались оба первых вопроса). По формуле (3.8)

.

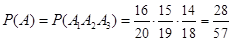События 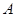и 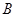называются независимыми (нужно не путать с несовместными), если выпол­няется условие

,

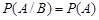(3.10)

или эквивалентное ему условие

(3.11)

На практике независимость событий означает, что появ­ление одного из них не изменяет вероятности другого или появление одного из них не несет информации, о другом.

События 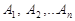называются независимыми, если каждое из них не зависит от каждого из остальных и от всевозможных произведений остальных событий.

Для независимых событий теорема умножения принимает простой вид

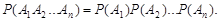
(3.12)

В частности, для двух независимых событий

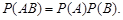
(3.13)

Дата добавления: 2015-06-26