Формула полной вероятности

Пример 3.18

Два стрелка стреляют по мишени. Вероят­ность попадания (событие A) для первого стрелка 0,7, ве­роятность попадания (событие В) для второго стрелка 0,8.

Считая попадания независимыми событиями, найти вероят­ность поражения мишени хотя бы одним стрелком (т, е. вероятность события ).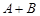

Решение

1-й способ. События 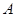и 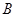совместны, поэтому следует воспользоваться формулой (3.15):

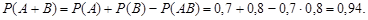
При подсчете вероятности произведения в силу независимости событи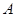й и 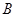, использовалась формула (3.14).

2-й способ. Сначала найдем вероятность противоположного события – промаха обоими стрелками 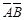. Полагая, что промахи также независимые события, имеем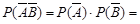 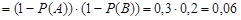(вос­пользовались следствием 5 пункта 3.4). Тогда .

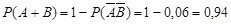Преимущества второго способа заметно проявляются в случае большого числа событий.

Пусть событие A может произойти только при осуществ­лении одного из событий 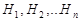(они называются ги­потезами), которые попарно несовместны и образуют прост­ранство элементарных событий некоторого испытания. Известны вероятности гипотез 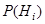и условные вероятности 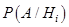( 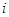=1, 2,...). Тогда вероятность события 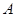находится по формуле полной вероятности:

.

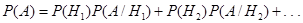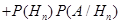(3.16)

Дата добавления: 2015-06-26