Пример 1.3

Нормальное распределение (закон Гаусса)

Пример 3.25

Найти наивероятнейшее число попаданий при четырех выстрелах в примере 1.1.

Решение. , .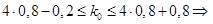

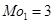При этом вероятности 3 и 4 попаданий одинаковы:

.

Нормальное распределение задается плотностью вероятности

(3.39)

Можно показать, что функция 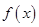удовлетворяет условию нормировки = 1.

Кривая имеет вид, изображенный на рис. 3.1.

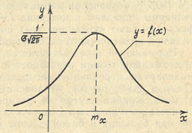Рис. 3.1.

Параметры 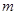и в формуле (2.20) являются соответственно математическим ожиданием () и средним квадратическим отклонением () нормально распределенной случайной величины .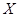

Кривая нормального распределения симметрична относительно линии , поэтому .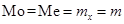

Введем функцию Лапласа

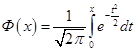
(3.40)

Таблица значений функции 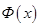приведена в прилож. 2. Свойства функции Лапласа

1) , т.е. 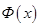монотонно возрастает.

2) ;

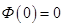3) ;

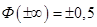4) , если ;

5) 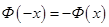, т.е. 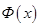нечетная функция.

Функция распределения для нормального закона находится через функцию Лапласа (2.21) по формуле

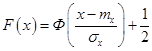
(3.41)

С помощью функции Лапласа находится вероятность попадания нормально распределенной случайной величины в заданный интервал:

(3.42)

Для интервала, симметричного относительно математического ожидания, формула (2.23) дает следующее:

или

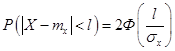
(3.43)

Если в формуле (2.24) положить 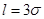, то получим

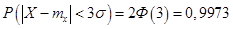
(3.44)

все (99,73%) значения нормально распределенной величины попадают в интервал 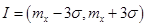. Этот факт называют «правилом трех сигм». Интервал I называется зоной практического рассеивания.

Нормальный закон встречается чаще всего в приложениях теории вероятностей. Им с большой моделируются реальные.распределения размеров и веса из­делий в одной партии, отклонения точек попадания снаряда от цели, ошибки измерений, распределение людей по росту, по интеллектуальным возможностям и т. д.

Шарики для подшипников отбраковываются так: если они проходят в отверстие диаметром , но не про­ходят в отверстие диаметром 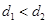, то признаются стандарт­ными. Пусть допуск, т. е. интервал , составляет 2/3 зо­ны практического рассеивания. Требуется предсказать долю шариков, прошедших отбраковку.

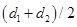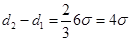Решение. Диаметр шарика – случайная величина Х, распределенная по нормальному закону с математическим, ожиданием и средним квадратическим отклонением . По условию . По формуле (3.24) находим

.

Таким образом, при назначенном допуске 95% изготовлен­ных шариков окажутся стандартными.

Дата добавления: 2015-06-26