Т р и к у т н и к и

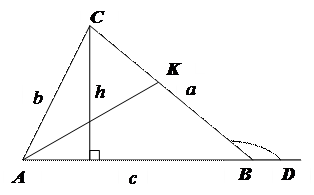Р І З Н О С Т О Р О Н Н І Й Т Р И К У Т Н И К

1. Нерівність трикутника: сума двох менших сторін трикутника завжди більша від більшої сторони: а + с > b.

2. Сума кутів трикутника 180°.

3. Зовнішній кут трикутника дорівнює сумі внутрішніх, не суміжних з ним:

Ð CВD = Ð А + Ð C.

4. Властивість бісектриси: .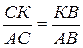

5. Теорема косинусів: с ² = a ² + b ² – 2 ab× cos Ð C.

6. Теорема синусів: .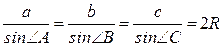

7. Периметр трикутника – це сума всіх його сторін: .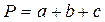

8. Середня лінія трикутника – це відрізок, який з’єднує середини двох сторін. Середня лінія трикутника паралельна до третьої сторони і дорівнює її половині.

9. Формули для знаходження площі трикутника:

, , , ,

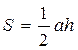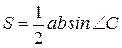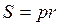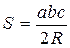формула Герона 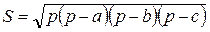, де .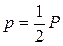

10. Радіус кола, описаного навколо трикутника (R), знаходиться на перетині серединних перпендикулярів всіх сторін, .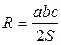

11. Радіус кола, вписаного у трикутник (r), знаходиться на перетині бісектрис всіх кутів, .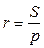

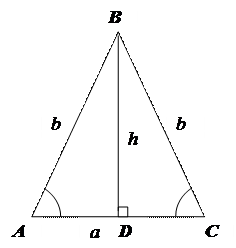
Р І В Н О Б Е Д Р Е Н И Й Т Р И К У Т Н И К

1. Основа – АС, бічні сторони рівні: АВ = ВС, кути при основі рівні: Ð А = Ð C.

2. Властивість рівнобедреного трикутника: ви-сота, проведена до основи є медіаною і бісек-трисою: ВD – висота, АD = DС, Ð АВD = Ð DВC.

3. Периметр трикутника: .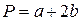

4. Формули для знаходження площі трикутника:

, .

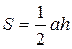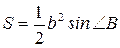5. Радіуси вписаного і описаного кіл: , .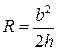

П Р Я М О К У Т Н И Й Т Р И К У Т Н И К

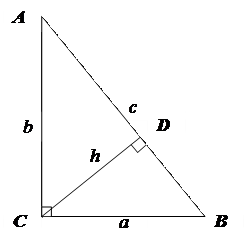
1. Гіпотенуза – АВ, катети: АС, ВС.

2. Сума гострих кутів – 90°: Ð А + Ð В = 90°.

3. Теорема Піфагора: 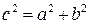або .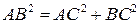

4. Трикутники АВС, АСD і СВD – подібні: , , .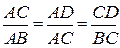

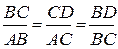5. CD – висота, проведена до гіпотенузи,

.

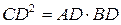6. Тригонометричні функції кута:

, , , ,

, , , .

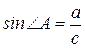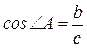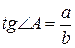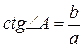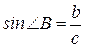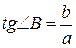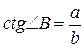6. Формули для знаходження сторін трикутника через тригонометричні функції кутів:

,

,

.

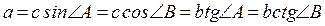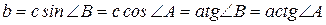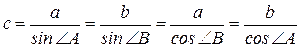8. Формули для знаходження площі: , .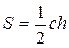

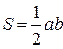9. Центр описаного навколо трикутника кола знаходиться на середині гіпотенузи.

10. Радіуси вписаного і описаного кіл: , .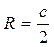

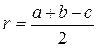П Р Я М О К У Т Н И Й Р І В Н О Б Е Д Р Е Н И Й Т Р И К У Т Н И К

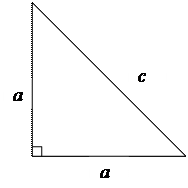1. Катети трикутника рівні, гострі кути дорівнюють по 45°.

2. Формули для знаходження катета і гіпотенузи цього трикутника: , .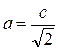

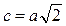3. Площа трикутника: , .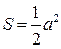

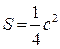4. Радіуси вписаного і описаного кіл: , .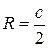

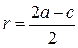Дата добавления: 2015-06-04