Нормально розподіленої випадкової величини

Інтервали довіри для оцінки середнього квадратичного відхилення

Інтервальні оцінки для математичного сподівання

Так, якщо σ відоме, Х – нормально розподілена випадкова величина або обсяг вибірки значний (n > 30), то ми можемо записати, що .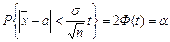

Тоді, якщо t = t _a = − розв’язок рівняння 2Φ(t) =a, то з надійністю a інтервал є інтервал довіри для математичного сподівання а. Значення t _a = t (a, n) шукаємо за допомогою таблицi 4.

Нехай ознака Х генеральної сукупності розподілена нормально. Знайдемо надійні межі для середнього квадратичного відхилення σ з заданою надійністю a. Оскільки точковою оцінкою для параметра σ є підправлене середнє квадратичне відхилення s, то для цього потрібно розв’язати рівняння: P{|σ − s |<δ } =a Û P{s −δ <σ < s +δ } =a.

Перетворимо подвійну нерівність s −δ <σ < s +δ

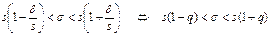
s (1 − q) < σ < s (1 + q) q < 1;

0 < σ < s (1 + q) q > 1,

де q=q(a,n) знаходимо за допомогою таблиці 5.

Дата добавления: 2015-06-04