Ошибки выборочного наблюдения

При проведении выборочного наблюдения нельзя получить абсолютно точные данные, как при сплошном обследовании. Обусловлено это тем, что наблюдению подвергается не вся совокупность, а только ее часть, поэтому выборочному наблюдению свойственна погрешность.

Ошибки подразделяются на ошибки регистрации и ошибки репрезентативности. Ошибки регистрации свойственны как сплошному, так и выборочному наблюдению Они являются следствием неправильного установления значения наблюдаемого признака или неправильной записи.

Ошибки репрезентативности присущи выборочному наблюдению и возникают в силу того, что выборочная совокупность не полностью воспроизводит генеральную. Ошибки репрезентативности подразделяются на случайные и систематические ошибки. Систематические ошибки связаны с нарушением принципов выборочной совокупности. Например, вследствие каких-либо причин, связанных с организацией отбора, в выборку попали единицы, характеризующие несколько большими или меньшими значениями признаков. В этом случае расчетные значения будут завышены или занижены.

Случайные ошибки обусловлены действием случайных факторов, которые возникают в результате несплошного характера наблюдения.

Избежать ошибок репрезентативности нельзя, однако, пользуясь мето­дами теории вероятностей, основанными на использовании предельных теорем закона больших чисел, эти ошибки можно свести к минимальным значениям.

Средняя ошибка выборки (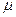) – это расхождение между средними выборочной и генеральной совокупности.

Чебышев: «С вероятностью сколь угодно близкой к 1 можно утверждать, что отклонение выборочной средней от генеральной средней может быть сколь угодно мало.

Средняя ошибка выборки зависит:

от объема выборки (чем больше численность при прочих равных условиях, тем меньше величина средней ошибки выборки);

степени варьирования признака (чем меньше вариация признака, а следовательно, и дисперсия, тем меньше ошибка выборки, и наоборот).

Предельная ошибка выборки – это максимально возможное расхождение между выборочной и генеральной средней, т.е. максимум ошибки при заданной вероятности ее проявления.

Предельная ошибка выборки – это максимально возможное расхождение выборочной и генеральной средних (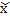 - 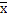), т.е. максимум ошибки при заданной вероятности ее появления.

Предельная ошибка выборки отвечает на вопрос о точности выборки с определенной вероятностью, значение которой определяется коэффициентом доверия t (в практических расчетах заданная величина, как правило не должна быть менее 0,95).

Применительно к нахождению среднего значения признака эта теорема может быть записана так:

Р[/ 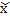- 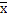/≤∆ 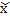]=t

где t – коэффициент доверия, который соответствует вероятности.

Р	0,683	0,954	0,990	0,997
t			2,58

Следовательно, с вероятностью 0,683 можно утверждать, что разность между выборочным и генеральными показателями не превысит средней ошибки выборки.

Предельная ошибка выборки (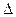) связана со средней ошибкой выборки 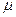отношением:

.

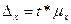При этом t как коэффициент кратности средней ошибки выборки зависит от значения вероятности Р, с которой гарантируется величина предельной ошибки выборки.

Формула для определения интервальной оценки генеральной средней:

Таким образом, заданной вероятностью можно утверждать, что значение генеральной средней можно ожидать в пределах от .

Формула для определения интервальной оценки генеральной доли:

При подготовке выборочного наблюдения с заранее заданными значениями допустимой ошибки выборки очень важно правильно определить объем (численность) выборочной совокупности.

Дата добавления: 2015-06-26