В зависимости от вероятности

Некоторые значения коэффициента доверия

Вероятность P или F(t)	0,683	0,950	0,954	0,970	0,997
Коэффициент доверия t	1,00	1,96	2,00	2,17	3,00

В практике выборочных обследований наибольшее распространение получили следующие типы выборки:

1) собственно-случайная;

2) механическая;

3) типическая;

4) серийная;

5) комбинированная.

Собственно-случайная выборка заключается в отборе единиц из генеральной совокупности наугад, без каких-либо элементов системности. Но прежде чем производить собственно-случайный отбор, необходимо установить четкие границы генеральной совокупности (например, при обследовании торговых предприятий необходимо убедиться, включит ли генеральная совокупность торговые павильоны, коммерческие палатки и пр.). Технически собственно-случайный отбор проводят методом жеребьевки или по таблице случайных чисел.

Механическая выборка состоит в том, что отбор единиц в выборочную совокупность из генеральной, в которой единицы расположены в определенном порядке (по алфавиту, по номеру и т.д.), производится таким образом, что заданное число единиц отбирается механически, через определенный интервал. При этом размер интервала в генеральной совокупности равен обратному значению доли выборки (при 2%-ной выборке отбирается каждая 50-я единица (1/0,02), при 5%-ной – каждая 20-я).

Для отбора единиц из неоднородной совокупности применяется типическая выборка. Все единицы генеральной совокупности разбиваются на несколько качественно однородных групп по признакам, влияющим на изучаемые показатели (например, при обследовании предприятий – отрасль, форма собственности).

Серийная выборка предполагает случайный отбор из генеральной совокупности не отдельных единиц, а их равновеликих групп (серий), в такой группе наблюдению подвергаются все без исключения единицы. Применение этого типа выборки обусловлено тем, что многие товары для их транспортировки, хранения и продажи упаковываются в пачки, ящики и т.д.

В практике статистического обследования помимо рассмотренных выше способов применяется и их комбинация. Так, например, можно комбинировать типическую и серийную выборки, когда серии отбираются в установленном порядке из нескольких типических групп. Возможна также комбинация серийного и собственно-случайного отборов, при которой отдельные единицы отбираются внутри серии в собственно-случайном порядке.

Конечной целью выборочного наблюдения является характеристика генеральной совокупности на основе выборочных результатов. Выборочные средние и относительные величины распространяются на генеральную совокупность с учетом предела их возможной ошибки.

Ошибка репрезентативности (ошибка выборки) представляет собой разность соответствующих выборочных и генеральных характеристик:

- для средней µ x = | x в - x |

- для доли µ w = | w - p |

Такая ошибка называется средней (теоретической). В каждой конкретной выборке расхождение между выборочной средней и генеральной может быть меньше средней ошибки выборки µ, равно ей или больше нее, причем каждое из этих расхождений имеет различную вероятность. Поэтому фактические расхождения между выборочной средней и генеральной можно рассматривать как некоторую предельную ошибку, связанную со средней ошибкой и гарантируемую с определенной вероятностью Р.

Предельные ошибки выборки для некоторых способов формирования выборочной совокупности см. таблицу 1.6.

Средняя ошибка для малой выборки исчисляется по формуле 1.20:

(1.20)

Предельная ошибка выборки Δ позволяет определить значения характеристик генеральной совокупности:

для средней 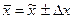; (1.21)

для доли p = w ± D w. (1.22)

При проектировании выборочного наблюдения с заранее заданным значением допустимой ошибки выборки очень важно правильно определить численность (объем) выборочной совокупности, которая с определенной вероятностью обеспечит заданную точность результатов наблюдения.

Формулы для определения необходимой численности выборки легко получить непосредственно из формул ошибок выборки (см. таблицу 1.6). Эти формулы показывают, что с увеличением предполагаемой ошибки выборки значительно уменьшается необходимый объем выборки.

Таблица 1.6

Дата добавления: 2015-06-26