Тема. Выборочное наблюдение

Определение ошибки выборочной доли.

При серийном бесповторном отборе средняя ошибка выборочной средней рассчитывается по формуле:

,

где — межгрупповая дисперсия доли;

При бесповторном отборе она рассчитывается по формуле:

,

Межгрупповая дисперсия определяется:

,

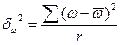
Комбинированный отбор. В практике статистических обследований помимо рассмотренных выше способов отбора применяется и их комбинация. Так, например, можно комбинировать типическую и серийную выборки, когда серии отбираются в установленном порядке из нескольких типических групп. Возможна также комбинация серийного и собственно-случайного отборов, при которых отдельные единицы отбираются внутри серии в собственно-случайном порядке.

1. Понятие о выборочном наблюдении.

2. Типы выборки.

3. Средняя ошибка выборки. Распространение результатов выборки на генеральную совокупность. Предельная ошибка выборки.

4. Необходимая численность выборки.

Статистическая методология исследования массовых явлений различает, как известно, два способа наблюдения в зависимости от полноты охвата объекта: сплошное и несплошное. Разновидностью несплошного наблюдения является выборочное.

Под выборочным наблюдением понимается такое несплошное наблюдение, при котором статистическому обследованию подвергаются единицы изучаемой совокупности, отобранные случайным способом.

Совокупность, из которой проводится отбор, называется генеральной, совокупность отобранных единиц – выборочной.

Применение выборочного наблюдения обусловлено следующими причинами:

1) экономия времени и средств в результате сокращения объема работ;

2) сведение к минимуму порчи или уничтожения исследуемых объектов (определение прочности пряжи при разрыве);

3) необходимость детального исследования каждой единицы наблюдения при невозможности охвата всех единиц (при изучении бюджета семей);

4) достижение большей точности результатов обследования благодаря сокращению ошибок, происходящих при регистрации.

Преимущество выборочного наблюдения по сравнению со сплошным можно реализовать, если оно организовано и проведено в соответствии с научными принципами теории выборочного метода– обеспечение случайности (равной возможности попадания в выборку) отбора единиц и достаточного их числа.

Соблюдение этих принципов позволяет достичь репрезентативности полученной выборочной совокупности.

Основная задача выборочного наблюдения в экономике состоит в том, чтобы на основе характеристик выборочной совокупности (средней и доли) получить достоверные суждения о показателях средней и доли в генеральной совокупности.

По методу отбора различают повторную и бесповторную выборки. При повторной выборке общая численность единиц генеральной совокупности в процессе выборки остается неизменной. Каждую единицу, попавшую в выборку, после регистрации снова возвращают в генеральную совокупность, и она сохраняет равную возможность со всеми прочими единицами при повторном отборе единиц вновь попасть в выборку. При бесповторной выборке единица совокупности, попавшая в выборку, в генеральную совокупность не возвращается и в дальнейшей выборке не участвует. Обычно выборку организуют по бесповторной схеме.

По степени охвата единиц совокупности различают большие и малые (меньше 30 единиц) выборки.

Основные характеристики параметров генеральной и выборочной совокупностей обозначаются символами:

N – объем генеральной совокупности;

n – объем выборки;

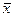– среднее значение признака в генеральной совокупности (генеральная средняя);

– выборочная средняя;

m – численность единиц, обладающих данным значением признака в выборке;

p – доля единиц, обладающих данным значением признака в общем числе единиц генеральной совокупности (генеральная доля);

w – выборочная доля;

s² – дисперсия признака в генеральной совокупности (генеральная дисперсия);

S² – выборочная дисперсия;

δ² – межгрупповая дисперсия в серийной выборке;

r – число отобранных серий;

R – общее число серий;

s – среднее квадратическое отклонения в генеральной совокупности;

S – среднее квадратическое отклонение в выборке;

К – доля выборки – отношение числа единиц выборочной совокупности к числу единиц генеральной совокупности;

µ – средняя ошибка выборки;

D – предельная ошибка выборки;

D% – предельная относительная ошибка выборки;

t – нормированное отклонение – «коэффициент доверия», зависящий от вероятности, с которой гарантируется предельная ошибка выборки (табл. 1.).

Таблица 1.

Дата добавления: 2015-06-26