Элементы И, И-НЕ, или, или-не

Следующий шаг на пути усложнения компонентов цифровой электроники — это элементы, выполняющие простейшие логические функции. Объединяет все эти элементы то, что у них есть несколько равноправных входов (от 2 до 12) и один выход, сигнал на котором определяется комбинацией входных сигналов.

Самые распространенные логические функции — это И (в отечественной системе обозначений — ЛИ), И-НЕ (обозначается ЛА), ИЛИ (обозначается ЛЛ) и ИЛИ-НЕ (обозначается ЛН). Присутствие слова НЕ в названии элемента обозначает только одно — встроенную инверсию сигнала. В международной системе обозначений используются следующие сокращения: АND — функция И, HAND — функция И-НЕ, ОR — функция ИЛИ, NOR — функция ИЛИ-НЕ.

Название самих функций И и ИЛИ говорит о том, при каком условии на входах появляется сигнал на выходе. При этом важно помнить, что речь в данном случае идет о положительной логике, о положительных, единичных сигналах на входах и на выходе.

Элемент И формирует на выходе единицу тогда и только тогда, если на всех его входах (и на первом, и на втором, и на третьем и т.д.) присутствуют единицы. Если речь идет об элементе И-НЕ, то на выходе формируется нуль, когда на всех входах — единицы (табл.1). Цифра перед названием функции говорит о количестве входов элемента. Например, 8И-НЕ — это восьмивходовой элемент И с инверсией на выходе.

Таблица 1: Таблица истинности двухвходовых элементов И, И-НЕ, ИЛИ, ИЛИ-НЕ

Вход 1	Вход 2	Выход И	Выход И-НЕ	Выход ИЛИ	Выход ИЛИ-НЕ

Элемент ИЛИ формирует на выходе нуль тогда и только тогда, если на всех входах нуль. Элемент ИЛИ-НЕ дает на выходе нуль при наличии хотя бы на одном из входов единицы (табл.1). Пример обозначения: 2ИЛИ-НЕ — двухвходовой элемент ИЛИ с инверсией на выходе.

И ИЛИ

И-НЕ ИЛИ-НЕ

Рис. 8. Обозначения элементов И, И-НЕ, ИЛИ, ИЛИ-НЕ: зарубежные (слева) и отечественные (справа)

Отечественные и зарубежные обозначения на схемах двухвходовых элементов И, И-НЕ, ИЛИ, ИЛИ-НЕ показаны на рис 8. Нетрудно заметить (см. табл.1), что в случае отрицательной логики, при нулевых входных и выходных сигналах, элемент И выполняет функцию ИЛИ, то есть на выходе будет нуль в случае, когда хотя бы на одном из входов нуль. А элемент ИЛИ при отрицательной логике выполняет функцию И, то есть на выходе будет нуль только тогда, когда на всех входах присутствуют нули. И так как в реальных электронных устройствах сигналы могут быть любой полярности (как положительные, так и отрицательные), то надо всегда очень аккуратно выбирать требуемый в каждом конкретном случае элемент. Особенно об этом важно помнить тогда, когда последовательно соединяются несколько разноименных логических элементов с инверсией и без нее для получения сложной функции.

Поэтому элементы И, И-НЕ, ИЛИ, ИЛИ-НЕ разработчику далеко не всегда удобно применять именно как выполняющие указанные в их названии логические функции. Иногда их удобнее использовать как элементы разрешения/запрещения или смешивания/совпадения. Но сначала мы рассмотрим случаи реализации именно логических функций на этих элементах.

На рис.9 приведены примеры формирования элементами выходных сигналов на основании требуемых временных диаграмм входных и выходных сигналов. В случае

а) выходной сигнал должен быть равен единице при двух единичных входных сигналах, следовательно, достаточно элемента 2И. В случае

б) выходной сигнал должен быть равен нулю, когда хотя бы один из входных сигналов равен единице, следовательно, требуется элемент 2ИЛИ-НЕ. Наконец, в случае

в) выходной сигнал должен быть равен нулю при одновременном приходе единичного сигнала Вх. 1, нулевого сигнала Вх. 2 и единичного сигнала Вх. 3. Следовательно, требуется элемент 3И-НЕ, причем сигнал Вх. 2 надо предварительно проинвертировать.

Рис. 9. Примеры применения элементов И и ИЛИ

Любой из логических элементов рассматриваемой группы можно рассматривать как управляемый вентиль входного сигнала (с инверсией или без нее).

Например, в случае элемента 2И-НЕ один из входов можно считать информационным, а другой — управляющим. В этом случае при единице на управляющем входе выходной сигнал будет равен инвертированному входному сигналу, а при нуле на управляющем входе выходной сигнал будет постоянно равен единице, то есть прохождение входного сигнала будет запрещено. Элементы 2И-НЕ с выходом ОК часто используют именно в качестве управляемых буферов для работы на мультиплексированную или двунаправленную линию.

Точно так же в качестве элемента разрешения/запрещения могут применяться элементы И, ИЛИ, ИЛИ-НЕ (рис.10). Разница между элементами состоит только в полярности управляющего сигнала, в инверсии (или ее отсутствии) входного сигнала, а также в уровне выходного сигнала (нуль или единица) при запрещении прохождения входного сигнала.

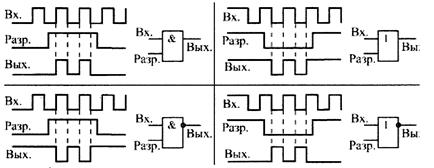
Рис. 10. Разрешение/запрещение прохождения сигналов на элементах И, И-НЕ, ИЛИ, ИЛИ-НЕ

Рис. 11. Появление лишнего фронта при запрещении входного сигнала

При использовании элементов разрешения/запрещения могут возникнуть дополнительные проблемы в случае, когда сигнал с выхода элемента идет на вход, реагирующий на фронт сигнала. В момент перехода из состояния разрешения в состояние запрещения и из состояния запрещения в состояние разрешения в выходном сигнале может появиться дополнительный фронт, никак не связанный с входным сигналом (рис. 11). Чтобы этого не произошло, надо придерживаться следующего простого правила: если вход реагирует на положительный фронт, то в состоянии запрещения на выходе элемента должен быть нуль, и наоборот.

1.5. Построение произвольной таблицы истинности.

Любая логическая схема без памяти (комбинационного тапа) полностью описывается таблицей истинности. При построении сложных логических схем с произвольной таблицей истинности используется сочетание простейших схем "И" "ИЛИ" "НЕ".

При построении схемы, реализующей произвольную таблицу истинности, каждый выход анализируется (и строится схема) отдельно. Для реализации таблицы истинности при помощи логических элементов "И" достаточно рассмотреть только те строки таблицы истинности, которые содержат логические " 1" в выходном сигнале. Строки, содержащие в выходном сигнале логический 0 в построении схемы не участвуют. Каждая строка, содержащая в выходном сигнале логическую "1", реализуется схемой логического "И" с количеством входов, совпадающим с количеством входных сигналов в таблице истинности. Входные сигналы, описанные в таблице истинности логической " 1" подаются на вход этой схемы непосредственно, а входные сигналы, описанные в таблице истинности логическим "0" подаются на вход через инверторы. Объединение сигналов с выходов схем, реализующих отдельные строки таблицы истинности, производится при помощи схемы логического ИЛИ. Количество входов в этой схеме определяется количеством строк в таблице истинности, в которых в выходном сигнале присутствует логическая "1".

Дата добавления: 2015-06-04