Вычисление моментов инерции во многих случаях можно упростить, используя соображения подобия и симметрии, а также теорему Штейнера

Рис. 4.1

Найдем связь между моментами инерции тела относительно двух неподвижных параллельных осей. Пусть оси перпендикулярны плоскости рисунка и проходят соответственно через точки О и А (все точки находятся в плоскости рис. 4.1).

Т еорема Штейнера: момент инерции тела относительно какой-либо оси равен моменту инерции его относительно параллельной оси, проходящей через его центр масс С, сложенному с величиной ma ², где а – расстояние между осями, m – масса тела.:

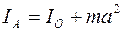, (4.4)

Далее вычисляют моменты инерции некоторых тел правильной формы.

1. Тонкий однородный стержень (длина l, масса m, Þ линейная плотность t=m/l=const):

а) ось вращения ОО^/ проходит перпендикулярно стержню через его центр масс С (рис. 4.2).

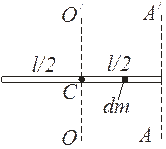
Рис. 4.2

В силу симметрии получают:

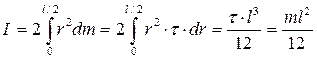; (4.5)

б) ось вращения АА^/ проходит перпендикулярно стержню через его конец. По теореме Штейнера (4.4) получают:

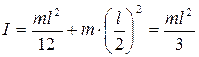. (4.6)

3. Однородное тонкое круглое кольцо (масса m, радиус R,).В силу симметрии очевидно (рис. 4.5), что

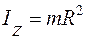, (4.10)

в силу симметрии

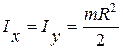. (4.11)

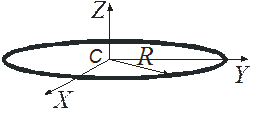
Рис. 4.5 Рис. 4.6

4. Однородный диск или сплошной цилиндр (масса m, радиус R, объемом V).Начало координат (пересечение) трех взаимно перпендикулярных осей располагают в центре масс цилиндра (можно аналогично случаю 2, а) сместить все вещество вдоль оси ОZ, т.е. получить тонкий диск малой толщины h^/, плотности r=m/V¢, V¢=p×R² h¢ – объем после смещения, см. рис. 4.6), для которого

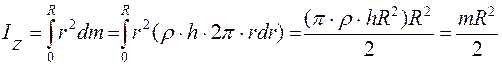. (4.12)

Согласно уравнению (4.8) имеют:

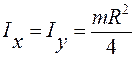. (4.13)

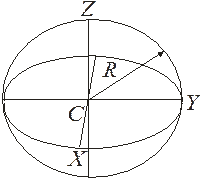
Рис. 4.7

5. Полый шар с бесконечно тонкими однородными стенками (сфера массы m, радиуса R).Расположим начало координат (пересечение) трех взаимно перпендикулярных осей в центре сферы, в ее центре масс С (рис. 4.7), тогда в силу симметрии и формулы (4.7):

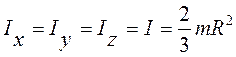. (4.14)

6. Сплошной однородный шар (масса m, радиус R, объем V).Расположим начало координат (пересечение) трех взаимно перпендикулярных осей в центре шара и рассмотрим шар как совокупность тонких сфер. Момент инерции такого тонкого сферического слоя по формуле (4.14) будет иметь вид:

,

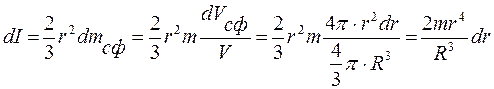тогда момент инерции шара:

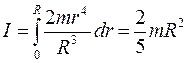. (4.15)

В некоторых задачах используется понятие момента инерции относительно точки. Поскольку ориентация различных элементов тела (ТТ) относительно его произвольной точки должна задаваться тремя координатами, то его инертность должна характеризоваться набором 9 чисел – тензором инерции (в математике используются скаляры – одно число, векторы – тройки чисел и тензоры – запись их представляет собой матрицу III порядка).

Если работа силы идет только на вращение тела, т.е. на увеличение кинетической энергии (КЭ) вращения, то

.

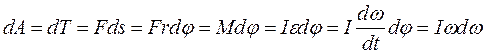При увеличении скорости вращения от 0 до w КЭ вращения равна

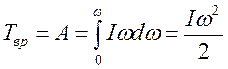. (4.26)

Дата добавления: 2015-06-04