Деформации твердых тел (ТТ)

Под механическими свойствами ТТ понимают их механическую реакцию (деформация) на внешнее воздействие: растяжение–сжатие, изгиб, кручение, удар и т.п. В результате внешнего силового воздействия в ТТ появляются напряженные состояния. Обычно оно появляется под действием поверхностных сил, действующих на выделенный элемент площади поверхности со стороны других тел, например, реакция опоры. Объемные силы, например, сила тяжести деформации, обычно деформаций и напряженных состояний не вызывают.

Отношение модуля поверхностной силы dF к площади воздействия dS называется напряжение м:

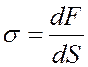. (14.1)

Различают истинные и условные напряжения. Для определения истинного напряжения необходимо учитывать изменение площади воздействия и, следовательно, приложенной внешней поверхностной силы. В общем случае напряженное состояние ТТ описывают с помощью тензора (матрицы) напряжений s_ij для учета анизотропности кристаллов (при этом учитываются элементы симметрии и различия механических свойств вдоль разных направлений).

Под действием напряжений ТТ может изменять свою форму, либо объем, но, как правило, и то, и другое меняется одновременно – ТТ деформируется. Основными видами деформации являются растяжение–сжатие и сдвиг, все остальные случаи могут быть получены посредством их комбинаций. Количественной мерой деформации является в простейшем случае так называемая относительная деформация 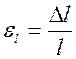или относительное поперечное растяжение (сжатие) 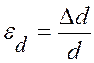, где l – длина стержня, d – его диаметр, D l – абсолютное удлинение (абсолютная деформация).

Экспериментально установлено, что, как правило, при деформации в одном направлении тело деформируется и в других направлениях (рис. 14.7). Поэтому величины e_l и e_d взаимосвязаны соотношением

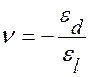, (14.2)

где n – коэффициент Пуассона, зависящий от природы (свойств) материала.

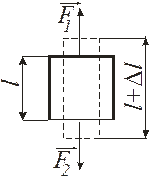
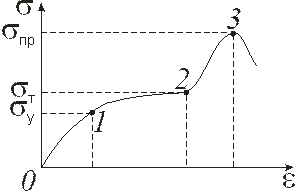
Рис. 14.7 Рис. 14.8

Общий вид зависимости s (e) напряжения от величины деформации e представлен на рис. 14.8. В зависимости от природы тел вид участков кривой различается углами наклона и протяженностью. Участок 01 – область упругой деформации: тело при снятии внешнего воздействия практически полностью восстанавливает свою форму и объем. Наибольшее значение s_y, соответствующее этому, называется предел ом упругости. При дальнейшем (s>s_y) незначительном росте напряжений вплоть до некоторого значения s _т – предел а текучести – деформация значительно увеличивается (область пластических деформаций – тело не восстанавливает свои размеры и форму). Пластические деформации не приводят к нарушению сплошности тела. Следует отметить интересное явление: если тело подвергнуть пластической деформации, а затем, сняв нагрузку, создать напряжение еще раз, то предел упругости увеличится. Это явление называется деформационным упрочнением. Если участок 12 значителен, то материал называют вязким, если мал – хрупким. Дальнейшее увеличение напряжений при значениях больших предел а прочности s _пр вызывает необратимое разрушение тела.

В достаточно узкой области, в которой величина деформации пропорциональна приложенному напряжению вплоть до некоторого значения напряжения, называемого пределом пропорциональности, выполняется (1660г.) закон Р. Гука (1635–1703):

- в случае деформации растяжения–сжатия

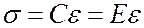, (14.3)

где Е – модуль (1807г.) Т. Юнга (1773–1829) – численно равен напряжению, требуемому для единичного удлинения стержня из данного материала;

- в случае сдвиговой деформации (рис.14.9)

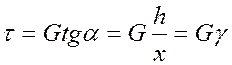, (14.4)

где t – касательное напряжение;

G – модуль вектора сдвига;

a – угол сдвига;

g – относительный сдвиг;

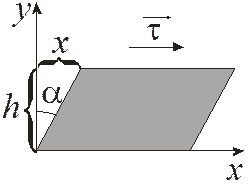
Рис. 14.9

1.12. элементы специальной теории относительности

В любой момент времени для точки m можно записать:

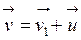. (6.3)

Выражение (6.3) – это классический закон сложения скоростей (правило сложения): скорость тела относительно неподвижной СО равна векторной сумме скорости тела относительно движущейся СО и скорости движущейся СО относительно неподвижной.

Специальная теория относительности (СТО) А. Эйнштейна базируется на двух постулатах:

1. Принцип относительности – во всех ИСО все физические явления протекают одинаково (обобщения принципа относительности Галилея на все законы природы).

2. Принцип инвариантности скорости света – скорость света в вакууме c не зависит от движения источника света или наблюдателя и одинакова во всех ИСО(утверждается как опытный факт).

В начале XX в. стало ясно, что уравнения физики должны быть пересмотрены. Стали предприниматься попытки записать уравнения движения и электродинамики так, чтобы они были инвариантны относительно перехода от одной СО к другой.

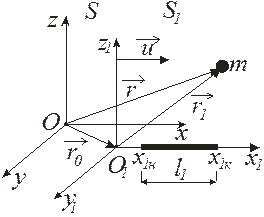
Рис. 6.2

Х. Лоренц (1853–1928) решил (1904г.), что если сделать следующие преобразования координат и времени, то уравнения (60 гг. XIX в.) Дж. Максвелла (1831–1879) будут инвариантны, т.е. не изменят своей формы (в случае направления скорости 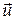вдоль параллельных осей Ох и О ₁ х ₁ (рис. 6.2)):

, ,

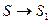
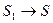
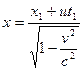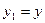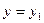, , (6.6)

, ,

. .

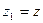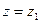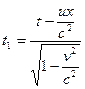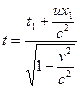Покажем относительный характер одновременности событий. Пусть система S ₁ движется со скоростью u относительно системы S, и в начальный момент времени t=0 их начала координат совпадают. Пусть в момент времени t= 0 в ИСО S источник излучает импульс света в направлении оси Ох. Тогда, дойдя до некоторой точки с абсциссой x, свет пройдет расстояние х=ct, а в системе S ₁ – x ₁= сt ₁; поскольку x ₁ ¹х (так как S ₁ движется относительно S со скоростью 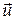= const), то и отсчет времени будет иметь относительный характер в силу относительности понятий «подвижная» и «неподвижная» СО.

В уравнениях (6.6) наблюдается симметрия (уравнения обратимы). Преобразования от S к S ₁ и обратно отличаются знаком перед u, что очевидно, поскольку, если S ₁ движется относительно S со скоростью u, то система S движется относительно S ₁ со скоростью (– u).

Это не означает, что описанное ниже замедление времени является кажущимся явлением. Правильнее говорить не об изменении хода времени в разных СО, а о различии протекания локализованного в пространстве временного процесса. Для того чтобы установить, какие часы отстают, необходимо «движущиеся» и «неподвижные» часы свести вместе. Но для этого необходимо или вернуть «движущиеся» часы, или ускорить «неподвижные». Очевидно, что результаты должны зависеть от характера сближения часов, т.к. ускорение абсолютно. Отстанут те часы, которые будут двигаться ускоренно. Именно этим объясняется меньшее старение близнеца–космонавта, вернувшегося на Землю, по сравнению с другим близнецом – жителем Земли.

Таким образом, преобразования Х. Лоренца удовлетворяют СТО, т.к. все физические явления описываются законами, не меняющимися при преобразованиях.А. Эйнштейн показал, что преобразования (6.6) имеют универсальный характер.

Преобразования Галилея (6.2) являются предельным случаем (6.6) при u<<c (формально в пределе при c ®¥) – в этом заключается суть принципа соответствия (каждая новая теория должна заключать в себе предыдущую в качестве частного случая), впервые введенного в научную методологию великим датским физиком Нильсом Бором (1885–1962).

Относительность времени:

а. Если два события ((1) и (2)) происходят одновременно (t ₁₍₁₎= t ₁₍₂₎) в СО S ₁ и x ₁₍₁₎= x ₁₍₂₎ (в одной и той же точке), то и в ИСО S t ₍₁₎= t ₍₂₎, x ₍₁₎= x ₍₂₎ (согласно формуле (6.6)); если же в СО S ₁ (t ₁₍₁₎= t ₁₍₂₎), но x ₁₍₁₎¹ x ₁₍₂₎, то в ИСО S не только x ₍₁₎¹ x ₍₂₎, но и t ₍₁₎¹ t ₍₂₎. Таким образом, события не только пространственно разобщены, но и не одновременны. В теории вероятности события, которые могут произойти одновременно, называют совместными. Для совместных событий как первое может предшествовать второму, так и второе первому в зависимости от координат и скорости u. Несовместными являются события, которые по каким-либо причинам не могут произойти одновременно, например, события, связанные друг с другом причинно-следственной связью, т.е. одно из событий является причиной (основанием) для наступления второго события (следствия), которое ни при каких обстоятельствах не произойдет раньше причины. Совместность/несовместность, причинно-следственные связи учитывают при релятивистском рассмотрении вопроса о том, какое из событий наступит раньше, а какое – позже.

б. Если длительность события (индексы: (1) – начало, (2) – конец события) в ИСО S D t = t ₍₂₎- t ₍₁₎, то в ИСО S ₁ 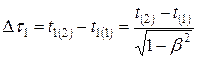, где b ²= (u/c) ², т.е. в движущейся ИСО S ₁ для того, чтобы событие завершилось, требуется время D t₁> D t (время идет медленнее в ИСО, относительно которой точка, где происходит событие, покоится).

Относительность линейных размеров вдоль направления движения (лоренцево сокращение длины). Пусть в движущейся ИСО S ₁ покоится стержень (рис. 6.2) длиной l ₁ =x _{1 к} -х _{1 н} («н» – начало, «к» – конец). Согласно формуле (6.6) 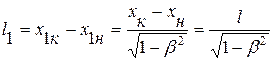, т.е. размеры стержня, измеренные в ИСО, относительно которой он движется, меньше длины, измеренной в ИСО, относительно которой он покоится: l ₁ >l.

Релятивистский закон сложения скоростей в СТО. Пусть в ИСО S ₁ тело имеет произвольно направленную скорость 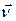, а ИСО S ₁ движется относительно ИСО S со скоростью 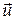, как показано на рис. 6.2. В случае, когда скорость v параллельна скорости u (n_y = n_z =0),

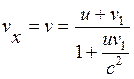. (6.8)

Формула (6.8) – релятивистский закон сложения скоростей. Для v<<c формально в пределе при c®¥ получаем классический закон сложения скоростей (6.3): 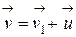. Если материальная точка движется со скоростью с (v ₁= c), тогда: 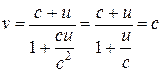. Согласно закону сложения скоростей, в теории относительности скорость тела не может быть больше скорости света, что согласуется со II постулатом А. Эйнштейна.

В релятивистскойдинамике масса тел есть функция их скорости:

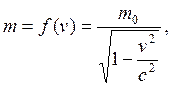(6.10)

где m₀ – масса покоя тела (частицы) в ИСО, относительно которой оно покоится (minimum);

m – масса в ИСО, относительно которой оно движется со скоростью v, т.е. масса различна в разных ИСО и с ростом скорости движения u – увеличивается.

В релятивистской динамике основной закон имеет вид (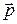 – релятивистский импульс):

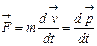или 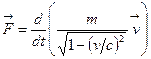. (6.11)

Уравнение (6.11) внешне совпадает с уравнением классической механики, т.е. инвариантно к преобразованиям Лоренца, тем самым удовлетворяя принципу относительности Эйнштейна. Важно отметить, что ни сила 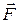, ни релятивистский импульс 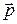не являются инвариантами. В общем случае вектор силы 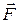не коллинеарен ускорению .

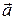Уравнение (6.11) справедливо и для проекций 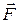на координатные оси F_x, F_y, F_z с учетом формул (6.7), (6.10) для проекций p_x, p_y, p_z релятивистского импульса .

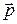В силу однородности и изотропности пространства в релятивистской механике также справедливы законы сохранения релятивистских импульса и момента импульса (в замкнутой системе). Разумеется, вблизи крупных гравитирующих (притягивающих) объектов эти свойства и законы могут нарушаться.

Полная энергия тела E, согласно А. Эйнштейну, пропорциональна массе:

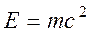. (6.16)

В формулу (6.16) не входит потенциальная энергия тела во внешнем силовом поле.

Получим выражение полной энергии как функцию релятивистского импульса (6.11):

,

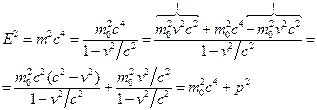т.е. 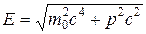. (6.17)

Формулу (6.15) можно записать в следующем виде:

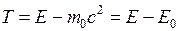. (6.18)

При v =0 и T =0, т.е. тело обладает энергией E = m ₀ c ², называемой энергией покоя.

Для характеристики устойчивости материи (например, устойчивости ядра как системы нуклонов), вводят понятие энергии связи. Энергия связи равна работе, которую надо совершить, чтобы разделить систему на составные части:

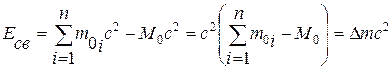, (6.19)

где m _{0 i} – масса покоя свободной частицы;

М ₀ – масса покоя системы, состоящей из n частиц;

D m – называется дефект ом массы (масса составляющих больше массы целого).

Энергию покоя и дефект масс обычно не учитывают при решении задач в механике, но исторически используют при расчете тепловых эффектов ядерных реакций. Теплота – одна из форм энергии, и закон взаимосвязи массы и энергии (6.16) был полностью подтвержден в экспериментах по определению теплоты, выделяющейся в ядерных реакциях.

Раздел 2. Молекулярная физика и термодинамика

Дата добавления: 2015-06-04