Распределения Максвелла и Больцмана

Несмотря на то, что скорости всех молекул в процессе хаотического движения непрерывно меняют значения и направления, средняя скорость 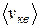остается постоянной при данной температуре (одна из статистических, проявляющихся при наличии большого числа частиц в системе, закономерностей). Это объясняется тем, что в состоянии равновесия реализуется некоторое стационарное распределение молекул по скоростям, подчиняющееся определенному статистическому закону. Этот закон был получен Дж.К. Максвеллом (1831–1879) на основе теории вероятности. Функция (распределения Максвелла молекул по скоростям) f(v) определяет относительное число (долю) молекул dN/N, скорости которых находятся в интервале [ v, v+dv ]:

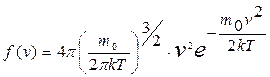. (9.16)

По сути, функция распределения молекул по скоростям f(v) равна вероятности dW встречи в газе молекулы со скоростью, заключенной в интервале [ v,v+dv ]:

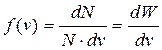. (9.17)

Вероятность же встречи молекулы со скоростью из интервала 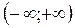– событие достоверное – равна 1, т.е.

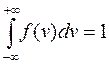. (9.18)

Уравнение (9.18) – условие нормировки.

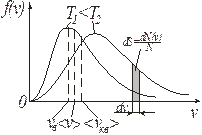
Рис. 9.4

Функция распределения всегда однозначна (вероятность не может иметь несколько значений для данного значения какого-то параметра), конечна (вероятность конечное число).

Подробнее о статистических закономерностях и функциях распределения см. в разделе «Элементы квантовой физики».

Максимум зависимости (и вероятности) f(v) (рис. 9.4) будет соответствовать наиболее вероятному значению скорости v_в. Данное значение можно получить, исследуя уравнение (9.16) на экстремум:

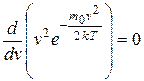, откуда ,

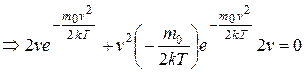что возможно при трех значениях:

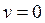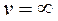, (min функции) и 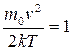(max функции – наиболее вероятная скорость), т.е.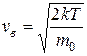

или 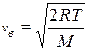. (9.19)

Для получения средней скорости используют методику, принятую в статистической физике: 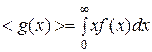. Подставляя x=v, f(x)=f(v) и dx=dv (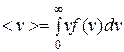) и интегрируя с использованием табличного интеграла

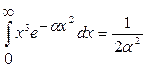, (9.20)

получают среднюю скорость:

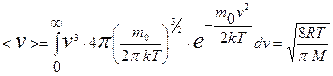. (9.21)

Из формул (9.13), ((9.19) и (9.21) следует, что 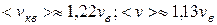(рис. 9.4).

Для получения функции распределения молекул по энергиям (e) необходимо в равенстве 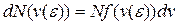(см. 9.20) провести, исходя из уравнения 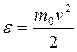, замены .

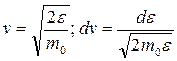Дата добавления: 2015-06-04