Момент силы и момент импульса

Вращение является составляющей большинства рассматриваемых в механике движений. Каждый день мы являемся свидетелями великого космического вращения. Данные последних теоретических исследований говорят, что всё вокруг и мы сами по свойствам напоминаем вращающиеся с большой частотой поля.

Динамические характеристики – момент силы и момент импульса, используемые при описании вращательного движения, играют в теории вращательного движения такую же большую роль, как ую сила и импульс играют в динамике поступательного движения.

Рис. 4.8

Известно, что передвинуть массивный предмет (например, ящик) вручную тяжело, гораздо легче передвинуть его с помощью длинной палки, трубы (лома), т.е. перекантовать с помощью рычага, причем, чем длинней этот рычаг, тем легче это сделать (прикладывается меньшая сила при большей длине рычага (см. рис. 4.8)). Вспомним знаменитое изречение Архимеда (ок. 286–212 гг. до н.э.): «Дайте мне точку опоры (и рычаг) и я переверну Землю».

Другой пример – взвешивание предметов на весах (см. рис. 4.9): при равных плечах (силы) весов l_i перевесит тот груз, масса которого m_i больше, а если массы грузов равны, то перевесит груз, для которого плечо силы l_i больше.

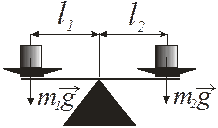
Рис. 4.9

Следует различать момент силы и момент импульса относительно точки и относительно оси, в первом случае – это вектора, а во втором – проекции векторов (скаляры).

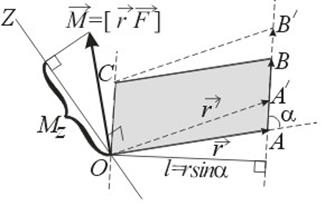
Рис. 4.10

Пусть дана точка О (полюс), относительно которой находится момент силы. Моментом силы 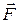относительно точки О называется векторное произведение (вектор) радиуса-вектора 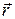, проведенного из точки О в точку А приложения силы на вектор :

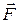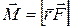(4.16)

Модуль момента силы:

, (4.17)

где l=rsina – кратчайшее расстояние до линии АВ действия силы (рис.4.10), называемое плечо м силы l.

При этом вектор 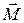не изменится, если точку приложения силы 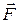перенести в любую другую точку, расположенную на линии действия силы, например в точку А^/. При этом параллелограмм ОАВС перейдет в параллелограмм ОА^/В^/С. Оба параллелограмма имеют одинаковые основание и высоту, а следовательно, и площадь.

В отличие от полярных векторов 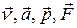(именно их изучают в школе), вектора, характеризующие вращательное движение 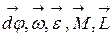, не имеют конкретной точки приложения (см. также лекция 1, п. 1), их называют скользящими. Так, вектор 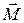можно откладывать от любой точки параллельно одному из направлений, полученному в результате векторного произведения (по свойствам векторного произведения 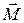перпендикулярно плоскости, в которой лежат два перемножаемых вектора – ), направление вектора 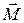совпадает с направлением поступательного движения правого винта при его вращении от вектора 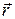к 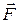(в математике термин – «левая тройка»).

Главным моментом 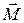нескольких внешних сил,действующих на систему, относительно точки О называется сумма моментов их относительно этой точки (принцип независимости действия сил):

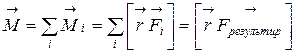, (4.18)

где силы 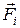считают приложенными к одной точке О, что можно получить путем параллельного переноса векторов 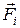(часто в механике для удобства при решении задач силы рассматривают как приложенные к центру масс тела, хотя это не для всех сил так, пример – сила трения 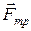приложена к поверхности тела).

При вращении ТТ (системы материальных точек) необходимо учитывать только внешние силы, так как внутренние силы взаимодействия двух любых элементов ТТ (системы) всегда равны по модулю (величине) и противонаправлены вдоль одной прямой (их векторная (геометрическая) сумма равна нулю).

Аналогично вышесказанному можно определить момент импульса относительно точки (вектор 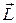) и относительно оси (проекция вектора L_z):

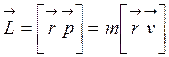, (4.19)

где 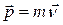– импульс (материальной) точки А, 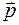. Важно отметить, что моментом импульса относительно точки может обладать и тело, движущееся поступательно (достаточно наличие импульса и плеча). Тело, обладающее импульсом, может не обладать моментом импульса относительно одних точек (в отсутствие плеча) и обладать относительно других.

Единицы измерения [М]=Н×м (не путать с [А]=Дж=Н×м), а .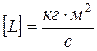

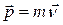В общем случае (неколлинеарна) и , т.е. и 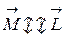, но если полюс (точка) О неподвижен, то импульс 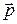точки А сонаправлен с ее скоростью 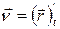, тогда:

,

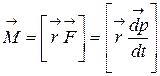т.к. ,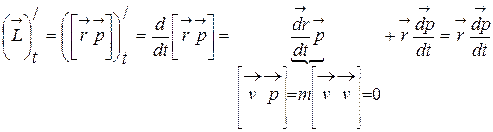

то есть получают основное уравнение динамики вращательного движения:

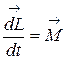. (4.20)

Этот закон остается справедливым и для системы материальных точек, в этом случае

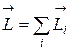и 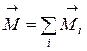. (4.21)

Особенность вращения ТТ, по сравнению с системой несвязанных друг с другом материальных точек, заключается в том, что при вращении ТТ вокруг неподвижной оси все его элементы движутся по окружностям, причем угловая скорость вращения 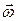для них одинакова (а линейная различная). Поэтому естественным будет выразить вектор 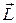через скорость .

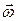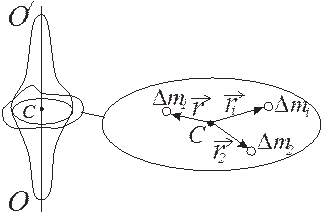
Рис. 4.11.

Разобьем ТТ (рис. 4.11), вращающееся относительно оси ОО ^/, на элементы (материальные точки). Момент импульса каждого элемента

.

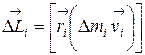С учетом равенства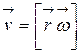

.

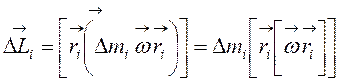В математике известно, что двойное векторное произведение имеет вид

,

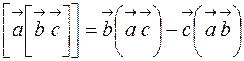т.е. .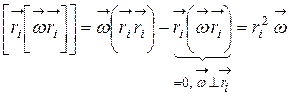

Таким образом,

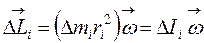, (4.22)

где DI_i – момент инерции i –го элемента.

Суммируя (интегрируя) по всем элементам, получают:

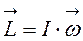. (4.23)

С учетом формул (4.20) и (4.23) получаем еще одну форму записи основного уравнения динамики вращательного движения:

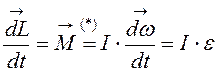, (4.24)

где e – угловое ускорение.

При вращении ТТ (системы материальных точек) необходимо учитывать только внешние силы, так как внутренние силы взаимодействия двух любых элементов ТТ (системы) всегда равны по модулю (величине) и противонаправлены вдоль одной прямой (их векторная (геометрическая) сумма равна нулю). Согласно уравнению (4.21) для замкнутой системы имеем:

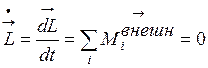, (4.25)

т.е. .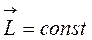

Значит, для замкнутых систем выполняется закон сохранения момента импульса.

Дата добавления: 2015-06-04