Элементы молекулярной кинетики. Явления переноса

Тогда

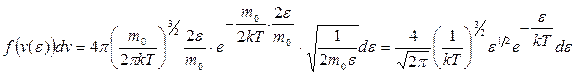
и 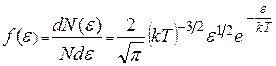. (9.25)

Находя среднее значение энергии аналогично (9.21), получают (9.1): .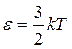

До сих пор считалось распределение молекул в пространстве равномерным. Однако в действительности это не так, поскольку молекулы газа всегда находятся в поле внешних сил, например, в поле тяготения. Силы тяготения удерживают атмосферу у поверхности земли, не давая ей рассеяться вследствие теплового движения в окружающем пространстве. В результате устанавливается некоторое стационарное распределение молекул, при котором давление и концентрация молекул (плотность) убывают с ростом высоты (атмосфера разрежается).

Найдем зависимости P=f(h) и n=f(h) в предположении однородного поля тяготения и постоянства температуры.

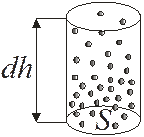
Рис. 9.5

Из уравнения Менделеева – Клапейрона

, .

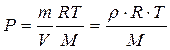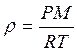Разность давлений на верхнее и нижнее основание мысленно выделенного цилиндра (рис. 9.5) равна весу столба воздуха, приходящемуся на единицу S основания, т.е. гидростатическому давлению P столбика dh:

.

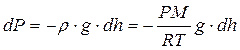Знак «–» показывает, что давление убывает с ростом высоты. Разделяя в данном дифференциальном уравнении переменные 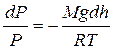и интегрируя 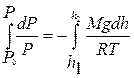, получают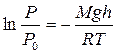

или 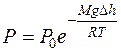(9.23)

Уравнение (9.23) – барометрическая формула Л.Больцмана (1844–1906 гг.).

Так как по условию рассмотрения T=const, то из формулы (9.23) с учетом равенства (9.12) получают зависимость n=f(h) для концентрации:

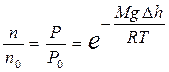Þ 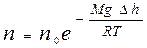. (9.24)

Распределение (9.24) можно переписать в другом виде с учетом равенств 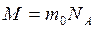и :

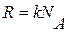, (9.25)

где U ₀ – потенциальная энергия молекулы во внешнем силовом поле (тяготения).

Конечные размеры молекул и высокая их концентрация приводит к тому, что в процессе хаотического теплового движения они непрерывно сталкиваются между собой, а в промежутках между двумя последовательными соударениями движутся равномерно и прямолинейно. Расстояние, которое проходит молекула между двумя соударениями, называется длиной свободного пробега. Эти расстояния могут быть сколь угодно различными, поэтому вводят понятие средней длины свободного пробега, которое является характеристикой всей совокупности молекул при данных P и T.

Минимальное расстояние d, на которое во время соударения сближаются центры двух молекул, называется эффективным диаметром молекулы.

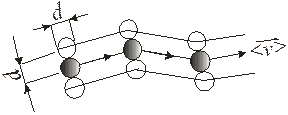
Рис. 10.1

Подсчитаем среднее число столкновений, испытываемых молекулой в единицу времени. «Заморозим» все молекулы, кроме рассматриваемой, тогда с последней столкнутся те молекулы, центры которых отстоят от траектории рассматриваемой молекулы на расстоянии r £ d. Рассматриваемую молекулу можно считать движущейся внутри ломаного цилиндра радиусом r (рис. 10.1). Среднее число столкновений в единицу времени, может быть найдено как число молекул, заключенных внутри, рассматриваемого цилиндра:

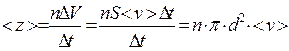. (10.1)

Вообще число столкновений должно зависеть от относительной скорости v_от молекул.

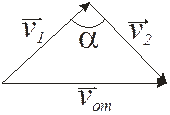
Рис. 10.2

Пусть скорости молекул до соударения 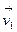и 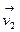соответственно. При столкновении угол (рис. 10.2) между данными скоростями может принимать любое значение: > 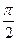; < 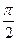, т.е. среднее значение функции <cos 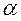> = 0. Относительная скорость 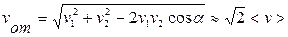. Поэтому уравнение (10.1) при учете движения других молекул следует записать в виде

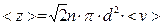, (10.2)

что точнее описывает действительность.

Из кинематики следует, что 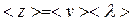, откуда средняя длина свободного пробега равна

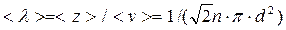. (10.3)

Хотя реальное строение молекул гораздо сложнее, зависимости (10.2) и (10.3) дают значение, хорошо согласующееся с опытным. Подход с использованием эффективных диаметра d и сечения молекул оказывается достаточно точным.

В 1827г. английский ботаник Р. Броун (1773–1858), наблюдая под микроскопом взвешенные в воде и газе частицы, обнаружил их непрекращающееся со временем непрерывное хаотическое (зигзагообразное) движение. Оживленность (интенсивность) названного впоследствии броуновским движения росла с увеличением температуры (т.к. уменьшается вязкость жидкости) и с уменьшением массы (размеров) взвешенных в жидкой или газообразной среде (броуновских) частиц независимо от химической природы их и среды. Французский ученый Ж. Перрен (1870–1942) наблюдал броуновское движение в двумерном случае – в плоскости – на поверхности мыльных пузырей.

Броуновское движение было объяснено на основе МКТ лишь спустя почти 80 лет как передача взвешенным в среде частицам импульса от сталкивающихся с ними в результате теплового движения молекул среды. Математическая теория броуновского движения была построена в 1905г. А.Эйнштейном (1879–1955) и в 1906г. М.Смолуховским (1872–1917).

Ранее были даны определение и свойства равновесного состояния и термодинамического (ТД) равновесия и ТД системы. Равновесные состояния реализуются в ТДС только в отсутствие потоков. Если существуют неоднородности – области, в которых значения характеризующих среду величин (концентрация (плотность), скорость частиц, температура среды) отличаются от значений в соседних областях, то возникают явления переноса – потоки вещества (диффузия), энергии (теплопроводность, теплопередача), импульса (внутреннее трение – вязкость). Под потоком обычно понимают передачу количества чего-либо (энергии, массы, импульса) в единицу времени через единичную площадку. Потоки при самопроизвольном (без внешнего воздействия) протекании процессов всегда направлены в сторону областей с меньшим значением энергии, концентрации (плотности) и импульса и приводят к выравниванию значений этих величин, характеризующих состояние среды.

Вследствие подобия условий все явления переноса описываются сходными по форме записи опытными законами. В общем виде можно записать:

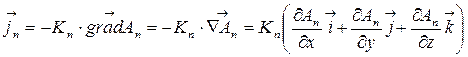, (10.5)

где 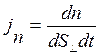– поток, соответствующей величины n (масса n 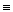m, энергии n 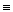Q, импульса n 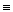v (скорость слоя) – величина, определяемая как количество n, переносимое в единицу времени перпендикулярно единичной площади сечения, через которое происходит перенос;

К_n – соответствующий коэффициент пропорциональности (коэффициент диффузии D, теплопроводности l, вязкости h;

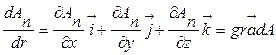– градиент соответствующего параметра, характеризующего среду (трехмерный случа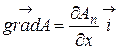й), или 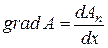(здесь и далее для простоты рассмотрим одномерный случай);

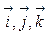– единичные направляющие вектора осей Ox, Оy, Оz соответственно (орты);

знак «–» означает, что поток направлен в сторону, противоположную направлению градиента.

Диффузия описывается законом Фика ():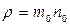

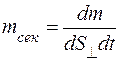или 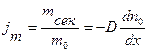. (10.6)

Следует различать концентрационную диффузию, вызванную неравновесным распределением частиц (в общем случае разной химической природы) в рассматриваемом объеме, и самодиффузию – броуновское (тепловое) движение собственных частиц вещества в заданном объеме этого вещества (даже в равновесных условиях), например, диффузия газа через проницаемую перегородку при условии, что газ по обе стороны перегородки уже абсолютно тождественен. При строгом расчете диффузионных потоков следует также учитывать и термодиффузию (1917г., С.Чепмен (1888–1970), Д.Энског). Например, если концы трубы, заполненной однородной смесью двух газов, имеют разные температуры, то вдоль трубы возникают противоположно направленные диффузионные потоки этих газов. Причем, молекулы большей массы стремятся перейти в более холодные области, а с меньшей – в более нагретые. Если же массы примерно одинаковы, а размеры разные, то в холодную область стремятся перейти более крупные молекулы, а в теплые – менее крупные. Коэффициент диффузии в уравнении (10.6) существенно зависит от температуры (D=f(T)).

Направление термодиффузионных потоков сильно зависит от характера взаимодействия между молекулами. Если молекулы считать силовыми центрами с радиусом действия ~ 1/r^a (отталкивание), то при переходе через а =5 потоки меняют свои направления на противоположные, а при а =5 термодиффузия исчезает. Строгая теория, описывающая термодиффузию, сложна, громоздка и выходит за рамки данного курса.

Теплопроводность – передача тепла от более нагретых областей к менее нагретым вследствие теплового движения молекул – описывается законом (1822 г., «Аналитическая теория тепла») Ж.Б.Ж. Фурье (1768–1830):

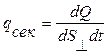или 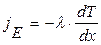. (10.7)

Передача импульса – вязкость, определяемая согласно уравнению (8.8), описывается законом И.Ньютона:

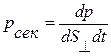
или 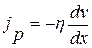. (10.8)

Если в газе или жидкости создать упорядоченное движение («ток»), то вследствие теплового движения скорости слоев с течением времени будут выравниваться. Вязкость – взаимопроникновение друг в друга, также обусловлена тепловым движением.

Строгая статистическая теория показывает, что характеристики D,l,h связаны простой пропорциональной связью, что подчеркивает единый механизм всех явлений переноса: h=r× D,

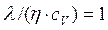. (10.9)

Таким образом, вышеперечисленные явления переноса неотделимы друг от друга, их следует рассматривать во взаимосвязи. Примером может служить (конвективный) теплообмен между потоками жидкости и поверхностью твердого тела (радиатора). Как правило, при этом возникает конвекция – восходящее движение нагретых слоев жидкости и нисходящее – охлаждаемых, т.е. происходит не только перенос тепла, но и массы (жидкости). В связи с этим в литературе часто пользуются понятием тепломассопереноса.

Дата добавления: 2015-06-04