Теплоемкость

Степени свободы. Внутренняя энергия идеального газа (ИГ), работа, количество теплоты. Первое начало термодинамики.

В общем случае под степенями свободы понимают минимальный набор параметров, с помощью которого можно полностью описать состояние системы (тела). Это могут быть независимые координаты, полностью описывающие положение тела (молекулы) в пространстве. Материальная точка, движущаяся в некоторой плоскости (xOy) имеет две степени (x, y), в пространстве – три степени свободы (x, y, z). Напомним, что в термодинамике (ТД) молекулы (многоатомные в общем случае) рассматриваются как система материальных точек (шариков, т.к. основная масса заключена в малом ядре), соединенных между собой жесткими недеформируемыми связями. Абсолютно твердое тело (АТТ) – (любая идеальная n -атомная молекула) – в общем случае имеет шесть степеней свободы: три координаты, описывающие положение центра масс; две координаты, определяющие в пространстве положение оси, проходящей через центр масс и некоторую фиксированную точку, угол поворота тела вокруг названной оси по отношению к некоторому начальному положению. Таким образом, АТТ обладает тремя степенями свободы поступательного движения и тремя степенями свободы вращательного движения. Если тело не АТТ и его части могут смещаться друг относительно друга, то необходимо рассматривать дополнительные степени свободы для описания колебательного движения.

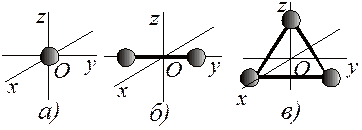
Рис. 11.1

В статистической физике показано, что средняя кинетическая энергия поступательного движения одноатомной молекулы ИГ 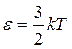((9.1) из (9.25)). Так как при хаотичном тепловом движении молекулы все три взаимноперпендикулярных направления движения равновероятны, то для одноатомной молекулы (рис. 11.1, а), имеющей три поступательные степени свободы (i =3), средняя кинетическая энергия на одну поступательную степень свободы равна

. (11.1)

Формула (11.1) выражает закон статистической физики – закон равномерного распределения энергии по степеням свободы, он справедлив для любой (n -атомной) молекулы.

Кинетической энергией вращения для одноатомной молекулы пренебрегают, т.к. для материальной точки радиус

.

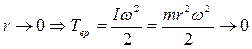Для двухатомной молекулы (рис. 11.1, б) к трем поступательным степеням свободы добавляются две вращательных, т.е. число степеней свободы i =5, а для многоатомной (три и более атомов, рис. 11.1, в) – три вращательных степени свободы (i =6). Нежесткая же двухатомная молекула имеет еще (плюс) одну колебательную степень свободы, а нежесткая трехатомная – еще три. Т.к. средняя кинетическая энергия гармонических колебаний примерно равна потенциальной энергии, то на каждую колебательную степень свободы приходится энергия .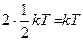

Таким образом, считая по-прежнему энергию одной степени свободы 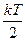, можно записать, что средняя энергия одной молекулы равна

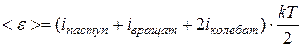, (11.2)

Полная энергия термодинамической системы (ТДС) состоит из кинетической энергии механического движения ТДС как единого целого и ее макрочастей: потенциальной энергии ТДС во внешних полях (гравитационном, электромагнитном) и внутренней энергии ТДС U.

Внутренняя энергия – энергия механического движения и взаимодействия (микро)частиц, составляющих (макро)ТДС, а также энергия электронных оболочек и взаимодействия нуклонов (протонов и нейтронов) в ядрах атомов. Однако для процессов, не сопровождающихся химическими или ядерными превращениями, можно считать последние составляющие внутренней энергии неизменными и не учитывать их. Поскольку получается, что выбор «точки» отсчета для внутренней энергии произволен, естественно, что она определяется с точностью до произвольной постоянной. Значение этой константы в большинстве случаев неважно, т.к. в законы физики, как правило, входит разность .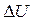

Зависимость вида 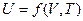называется калориметрическим уравнением.

Т.к. в ИГ пренебрегают силами взаимодействия между молекулами и считают их связи жесткими (т.е. отсутствуют колебания), то внутренняя энергия ИГ – это кинетическая энергия поступательного и вращательного движения его молекул; с учетом формул (11.1) и (11.2) для произвольного количества вещества получают:

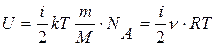. (11.3)

Внутренняя энергия является однозначной функцией состояния ТДС, т.е. не зависит от способа (пути) перехода ТДС в это состояние, а лишь от значения параметров, характеризующих данное состояние (обычно P, V, T). Согласно уравнению (11.3) внутренняя энергия ИГ не зависит от его объема – закон Д.П.Джоуля (1818–1889). Передачу энергии между телами (ТДС) и, следовательно, изменение их внутренней энергии можно осуществлять через работу и теплопередачу (теплота – эквивалент энергии). При этом энергия механического движения может превращаться в тепловую и наоборот. В отличие от внутренней энергии понятия работы и теплопередачи употребляют всегда в контексте с описанием способа изменения состояния ТДС, например, работа адиабатического сжатия ИГ нагрев ИГ (сообщение теплоты) и его изобарное расширение.

Первое начало термодинамики является эмпирически (опытно) установленным законом и, по сути, частным случаем закона сохранения энергии (XIX в.):

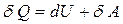. (11.4)

Формула (11.4) – вся теплота, сообщенная ТДС, идет на изменение ее внутренней энергии и на работу ТДС против внешних сил (знак «d» – обозначение полного дифференциала, его определение и свойства см. математику). Для ИГ положительной считается работа расширения ИГ, отрицательной – работа сжатия, в общем случае:

и 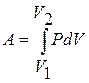. (11.5)

Если постоянен объем, т.е. процесс – изохорный, то из уравнений (11.4) и (11.5) , если же постоянно давление, т.е. процесс – изобарный, то

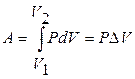и .

Удельная теплоемкость – теплота, которую надо сообщить 1 кг вещества для повышения его температуры на 1 К:

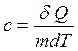, (11.10)

где т – масса вещества.

Пользуются также понятием молярной теплоемкости (для одного моля вещества):

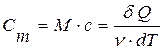, (11.11)

где М – молярная масса вещества, v – количество молей вещества.

Если известны удельная и молярная теплоемкость вещества, то теплоемкость конкретного тела можно определить как или .

Различают теплоемкости при постоянном давлении и при постоянном объеме. Для ИГ, рассматривая уравнение (11.4) совместно с уравнением (11.3) и (11.5), получают, что при постоянном объеме молярная теплоемкость равна

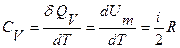, (11.12)

а при постоянном давлении -

. (11.13)

Уравнение (11.13)- уравнение Ю.Р.Майера (1814–1878): выводится с учетом уравнения Менделеева–Клапейрона РV_m=RT и РdV_m+V_mdР= РdV_m=RdT при постоянном давлении.

При сравнении уравнений (11.12) и (11.13) видно, что молярная теплоемкость при постоянном давлении больше, т.к. часть подводимой теплоты расходуется еще и на совершение ИГ работы расширения (против внешних сил).

На практике часто используют отношение теплоемкостей 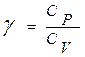(показатель адиабаты или показатель Пуассона). Так как и 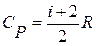_, то для одноатомного газа i =3 и показатель адиабаты 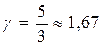; для двухатомного i =5 и показатель Пуассона 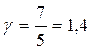; для трех- и более – i =6 и .

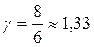Приведенные выше рассуждения классической (не квантовой) теории теплоемкости справедливы лишь для ИГ, т.е. в ряде частных случаев, и потому ограниченно применимы.

Дата добавления: 2015-06-04