Механика жидкостей

Раздел механики, изучающий движение жидкой среды и ее взаимодействие с твердыми телами, называется гидродинамикой (воздушной – аэродинамикой). Движение среды (жидкости, газа) называют течением, а саму движущуюся среду – потоком. Условия массопереноса при течении среды называются режимом течения. Режим течения, при котором вектор скорости в каждой точке постоянен по модулю и направлению, называется стационарным или установившимся, иначе – нестационарным. Существуют различные способы классификации течений, например, по специфике поверхностей, ограничивающей область течения: течение жидкости со свободной поверхностью, с поверхностью раздела, вдоль проницаемой границы и т.п., что позволяет кратко описывать свойства этих течений и указывать методы их исследования.

Рис. 8.1

Линия тока – мысленно проведенная в потоке линия, касательная, в каждой точке которой совпадает по направлению с вектором скорости жидкости в этой точке. Линии тока, проходящие через замкнутый контур, образуют трубку тока (рис. 8.1). Часть (или весь) потока, ограниченного трубкой тока называется струйкой тока.

Отвлекаясь от строения среды, ее часто представляют сплошной, несжимаемой и без внутреннего (см. ниже) трения (в гидродинамике это – модель идеальной жидкости (плотность жидкости слабо зависит от давления)).

В отличие от твердых тел, жидкости и газы в состоянии равновесия обычно не обладают упругостью формы, а лишь упругостью объема. Это значит, что газ и жидкость принимают форму сосуда, в котором находятся, но жидкость имеет определенный объем, а газ занимает весь объем сосуда, в котором находится (плотность газов сильно зависит от давления, а жидкостей – слабо). Исключение составляют жидкие пленки и поверхностные слои жидкости, где большую роль играет поверхностное натяжение. Механические свойства газов и жидкостей таковы, что приложение сколь угодно малой касательной силы приводит к значительным смещениям их частиц друг относительно друга – в связи с этим говорят о текучести жидкостей и газов.

Отношение нормальной силы, действующей на единицу площади, называется давление м жидкости (газа): p=F/S (единица измерения Паскаль: 1Па=1Н/м²).

Рис. 8.3

Рассмотрим, как влияет вес жидкости на распределение давления внутри покоящейся жидкости. При равновесии жидкости давление по горизонтали всегда одинаково, иначе равновесие отсутствовало бы. На основании вышесказанного можно сформулировать закон Б. Паскаля (1623–1662): давление в любом месте покоящейся жидкости одинаково по всем направлениям (горизонтальным плоскостям) и одинаково передается по всему объему, занятому покоящейся жидкостью. Поэтому свободная поверхность покоящейся жидкости всегда горизонтальна вдали от стенок сосуда.

Если жидкость несжимаема, то ее плотность r не зависит от давления, тогда при поперечном сечении столба жидкости S и его высоте h (глубине погружения):

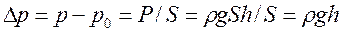, (8.1)

где P – вес столба; p – давление на нижнее основание мысленно выделенного в жидкости цилиндра; p₀ – давление на верхнее основание мысленно выделенного в жидкости цилиндра (атмосферное на поверхности, где h =0).

Давление Dр называется гидростатическим, оно линейно растет с глубиной (рис. 8.3).

Некоторые твердые тела могут находиться в равновесии в жидкости, т.е. существует противоположно направленная весу тела выталкивающая сила, обусловленная гидростатическим давлением жидкости (рис. 8.4).

Эта сила названа архимедовой (Архимед (ок. 286–212 гг. до н.э.)). Согласно закону Архимеда

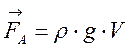, (8.2)

Рассмотрим стационарный поток жидкости в трубе. Массы жидкости, проходящие через любое из поперечных сечений трубки тока в единицу времени, равны (см. рис. 8.5):

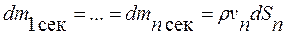. (8.3)

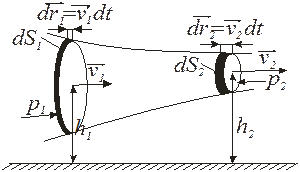
Рис. 8.5

Уравнение (8.3) называется уравнением неразрывности. Так как жидкость плохо сжимаема и ее плотность r практически не зависит от давления, то будут равны и секундные объемные расходы:

.

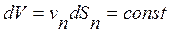Закон изменения механической энергии применительно к установившемуся течению идеальной жидкости

(8.6)

Уравнение (8.6) называется уравнением (1738г.) Д. Бернулли (1700–1782), где слагаемые называют: p – статическое, rgh – гидростатическое, – динамическое давление (скоростной напор). Сумму 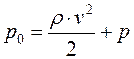называют полным давлением.

Из уравнения (8.3) следует, что на участках горизонтально расположенной трубки тока (горизонтальной трубы) с меньшей площадью поперечного сечения скорость потока будет больше, и наоборот, а из уравнения (8.6) с учетом этого следует, что статическое давление больше в широких местах, где скорость меньше, и наоборот.

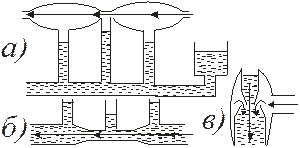
Рис. 8.6

Например, (рис. 8.6, а) жидкость поднимется выше в манометрическом колене (манометре), соединенном с узким местом трубы, по которой идет стационарный поток газа (трубка, содержащая короткий участок меньшего сечения, называется трубкой Вентури); уровень жидкости в манометре (рис. 8.6, б), соединенном с узким местом трубки Вентури, меньше. Из рис. 8.6, а и 8.6, в ясно, что вода может увлекаться потоком газа, а газ – откачиваться из сосуда за счет увлечения потоком воды до p =100 мм.рт.ст. (1 мм.рт.ст.=133,32 Па).

Возникновение внутреннего трения (вязкости) связано с передачей друг другу импульса частицами слоев среды, движущимися с различной скоростью и взаимодействием между самими частицами среды. Таким образом, один слой ускоряет второй, а второй, напротив, – тормозит первый с силой, определяемой закон ом И. Ньютона для внутреннего трения:

или , (8.8)

где Dn (dn) – разность скоростей соприкасающихся слоев (изменение скорости в направлении внешней нормали );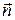

Dn/Dx (d n/dn) градиент (быстрота изменения) скорости в направлении Ох (скорость сдвига), перпендикулярном вектору скорости ;

S – площадь соприкосновения (чем больше площадь соприкосновения, тем больше сила);

t – касательное напряжение (создаваемое касательной силой трения F);

h – коэффициент пропорциональности – динамическая вязкость или просто вязкость [Па×с] (j =1/ h называется текучестью).

Величина x=h/r называется кинематической вязкостью, где r – плотность жидкости.

Единицы измерения динамической вязкости в системе СИ – Па×с, кинематической – м ²/ с. Иногда встречаются значения, указанные в «старой» системе единиц СГС: для динамической вязкости – Пуаз (П, P), для кинематической – Стокс (Ст, St), 1 Ст =10^-4 м ²/с.

Для характеристики типа течения вводят понятие

– число О. Рейнольдса (1842–1912);

где n ₀ – характерная скорость потока (значение или функция скорости, с помощью которой удобно описывать поведение потока, например, натекание из бесконечности); d – диаметр трубы.

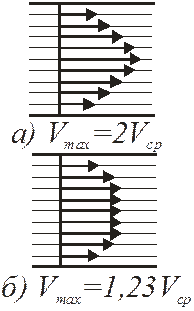
Рис. 8.8

Ламинарным (слоистым) называют течение, когда частицы жидкости движутся вдоль прямолинейных траекторий, параллельных оси трубы (параллельные слои не перемешиваются, все характеристики течения практически неизменны). Это течение характеризуется малым числом Re <1000, наблюдается при малых скоростях течения. При 1000£ Re £2000 наблюдается неустойчивость – переход от ламинарного к турбулентному (вихревому) течению, характеристики которого быстро и нерегулярно изменяются во времени (флуктуируют), параллельные слои перемешиваются. При дальнейшем росте Re течение турбулентно. При описании течения жидкости в трубе используют приближение пограничного слоя: слой жидкости, примыкающий к стенке трубы, остается неподвижным, скорости последующих слоев возрастают и достигают максимума у оси трубы.

Причина этого – прилипание частиц жидкости за счет вязкости. Толщина пограничного слоя d не остается постоянной и зависит от свойств жидкости, формы обтекаемого тела, места на этом теле (передняя (лобовая, здесь d меньше) или задняя часть обтекаемого тела (здесь больше)). На рис. 8.8 изображены профили усредненной скорости слоя при течении жидкости в трубе: а) ламинарном; б) турбулентном.

Для определения значения вязкости используют метод Стокса. Измеряя скорость n равномерного падения металлического шарика в жидкости, используют

. (8.19)

Дата добавления: 2015-06-04