Вычисление площадей плоских областей

Приложения двойных интегралов

Примеры для самостоятельной работы

Исследовать, сходятся ли двойные несобственные интегралы:

52. 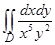, где D определена неравенствами х ³ 1, ху ³ 1;

53. , где D ограничена линиями у = 0, у = х², х² + у² = 1 (х ³ 0);

54. 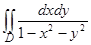, где D ограничена линиями х = 0, у = 0, х + у = 1;

55. , где D определена неравенством х² + у² £ х;

56. 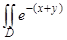, где D определена неравенством 0 £ х £ у.

Рассмотрим различные группы приложений для двойных интегралов.

Площадь S плоской области D равна двойному интегралу от дифференциала площади dS, распространенному на область D:

.

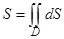В прямоугольных координатах элемент площади dS выражается формулой dS = dxdy, поэтому

.

Если область D определена, например, неравенствами , , 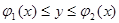то

. (24)

Так как в криволинейных координатах элемент площади dS = |J(u, v)|dudv, где J(u, v) – якобиан преобразования x = j (u, v), y = y (u, v), переводящего область D в область D, то площадь последней

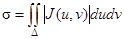. (25)

В частности, если в полярных координатах область D определена неравенствами 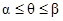, j(q) £ r £ y(q), то

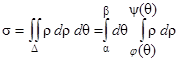. (26)

Пример 25. Вычислить площадь области, ограниченной линиями х = у² + 1, х = 5.

Данная область ограничена параболой х = у² + 1 и прямой х = 5 (рис. 39). Решая систему уравнений х = у² + 1, у = 0, находим точку А (1, 0) пересечения параболы с осью Ох. Из системы уравнений х = у² + 1, х = 5 находим две точки пересечения параболы с прямой х = 5 – В (5, 2), С (5, -2). Область АВС является как областью первого типа, так и областью второго типа.

Применяя формулу (24) и рассматривая область АВС как область первого типа, находим

В

		Рис. 40

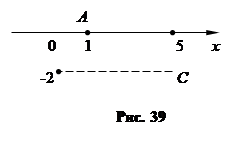Замечание. Рассматривая область АВС как область второго типа, получаем

.

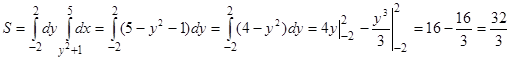Пример 26. Вычислить площадь области, ограниченную линиями у = 2 – х², у³ = х². Область, ограниченная указанными линиями, изображена на рис. 17 (область ОМ₁АМ₂).

По формуле (24)

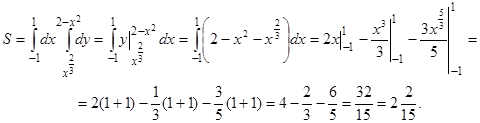
Пример 27. Вычислить площадь фигуры, ограниченной линией

.

В силу симметрии кривой относительно осей координат (рис. 40) достаточно вычислить площадь одной четверти данной фигуры (например расположенной в первом квадранте). Переходим к полярным координатам, полагая , 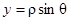. Полярное уравнение лемнискаты

, или .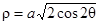

Для указанной части фигуры имеем: , , , .

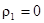Обозначая площадь этой части через s ₁, по формуле (26) получаем

.

Следовательно, площадь всей фигуры .

Пример 28. Найти площадь фигуры, ограниченной линией

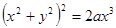(а > 0).

Из уравнения видно, что линия симметрична относительно оси Ох (уравнение не меняется от замены у на – у). Линия проходит через начало координат (х = 0, у = 0 удовлетворяют уравнению) и целиком расположена справа от оси Оу (х не может принимать отрицательных значений, так как левая часть уравнения неотрицательна). Линия расположена в ограниченной части плоскости (из уравнения видно, что х ⁴ £ 2 ax ³, поэтому х £ 2 а, а поскольку и у ⁴ £ 2 ax ³, то также и | y | £ 2 а). Кривая пересекает ось Ох при х = 0 и х = 2 а (рис. 41).

		Рис. 41

Введем полярные координаты. Тогда .

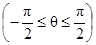Учитывая симметрию кривой, по формуле (26) находим

.

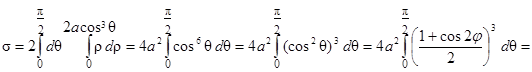
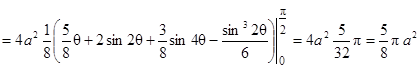Пример 29. Найти площадь фигуры, ограниченной линиями у² = 2 рх, у² = qx, у = ах, у = bх (0 < p < q, 0 < a < b).

Фигура представляет собой криволинейный четырехугольник, ограниченный двумя параболами и двумя прямыми, проходящими через начало координат (рис. 42).

Введем новые криволинейные координаты u, v, связанные с координатами х и у формулами:

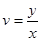
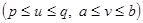, . (27)

Эта замена переменных подсказана видом области интегрирования (в качестве новых переменных взяты параметры, входящие в уравнения линий, ограничивающих данную фигуру). Из уравнений (27) выражаем х и у через u и v:

, . (28)

Находим якобиан преобразования (28):

.

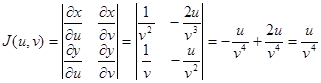По формуле (25)

Пример 30. Вычислить площадь фигуры, ограниченной линией

.

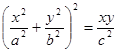Линия эта ограничена, симметрична относительно начала координат, так как уравнение ее не меняется при одновременной замене х на – х и у на – у, проходит через начало координат (эта точка является единственной точкой пересечения с осями координат), две симметричные петли ее лежат: одна – в первом координатном угле, другая – в третьем (ибо только в этих четвертях ху ³ 0 и только при этом условии уравнение имеет смысл).

Введем новые координаты («обобщенные» полярные координаты), которые связаны с декартовыми формулами: , 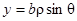. Уравнение кривой в новых координатах: .

Учитывая симметрию кривой и принимая во внимание, что , по формуле (25) находим

.

Пример 31. Найти площадь фигуры, ограниченной линией

(x > 0, y > 0).

Введем новые координаты по формулам: , 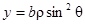. (Это возможно, так как x > 0, y > 0). Уравнение кривой примет вид

.

Исключая двойную точку в полюсе (r ² = 0), находим

.

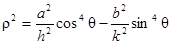Полученное уравнение, как и исходное, свидетельствует о том, что равенства возможны, когда правые части уравнений неотрицательны, т.е. , .

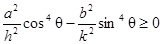Из последнего неравенства находим: , .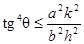

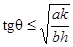Это означает, что в задаче рассматривается та дуга кривой, которой соответствует изменение угла q от до .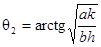

Так как

,

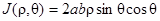по формуле (25) находим

Чтобы упростить полученный результат, положим . Тогда

, , .

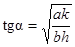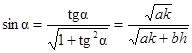Итак .

Дата добавления: 2015-06-04