Замена переменных в двойных интегралах

Задача вычисления двойного интеграла зачастую связана с необходимостью замены переменных. Рассмотрим двойные интегралы в полярных координатах.

Криволинейные координаты на плоскости. Рассмотрим непрерывно дифференцируемые функции u и v прямоугольных декартовых координат х и у:

u = j (x, y), v = y (x, y). (12)

Предположим, что уравнения (12) однозначно разрешимы относительно х и у:

x = j ₁(u, v), y = y ₁(u, v),(13)

где j ₁(u, v), y ₁(u, v) – непрерывно дифференцируемые функции u и v.

Придавая поочередно u и v различные (возможные для них) постоянные значения, получаем два семейства линий на плоскости (рис. 21); эти линии называются координатными линиями. Положение точки М на плоскости определяется парой чисел (х, у) или парой чисел u, v, где u и v выражены формулами (12). Пара чисел u, v называется криволинейными координатами точки М на плоскости.

x = const

у

j = const

у

Примером криволинейных координат являются полярные координаты, в этом случае u = r, v = j. Координатные линии – концентрические окружности и полупрямые, исходящие из начала координат (рис. 22). Прямоугольные координаты – также частный случай криволинейных: u = x, v = y. Координатные линии – прямые, параллельные осям координат (рис. 23).

		Рис. 22		Рис. 23

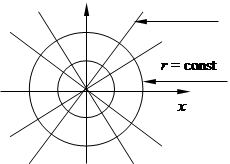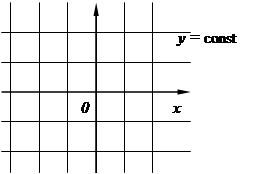Замена переменных в двойных интегралах. Если непрерывно дифференцируемые функции (13) устанавливают взаимно однозначное и в обе стороны непрерывное соответствие между точками области D плоскости Оху и точками области D плоскости Ouv (рис. 24), то

v

y

, (14)

где J(u, v) – функциональный определитель Якоби (или якобиан),

.

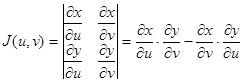Замену переменных в двойном интеграле рекомендуется производить так, чтобы упрощались подынтегральное выражение и область интегрирования.

Двойные интегралы в полярных координатах. В случае перехода к полярным координатам x = r cos j, y = r sin j формула (14) принимает вид

, (15)

так как модуль функционального определителя в этом случае

.

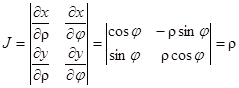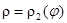
Если область D (рис. 25 – 27) ограничена лучами, образующими с полярной осью углы j ₁ = a, j ₂ = b, и кривыми , , 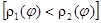то

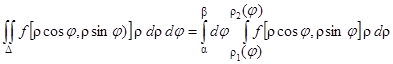. (16)

Если область D охватывает начало координат, то

.

Пример 13. Вычислить , где область D - круговой сектор, ограниченный линиями j = 0, 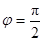, r = 2 (рис. 28).

		А

	D
		r
		Рис. 28		Рис. 29

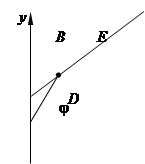Применим формулу (16). В данном случае , , r ₁( j ) = 0, r ₂( j ) = 2. Указанный круговой сектор – частный случай области D, точки А₁ и В₁ совпадают с точкой О (рис. 27).

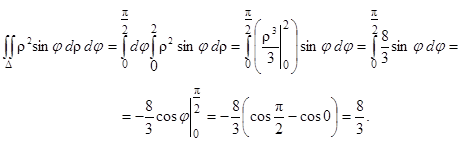
Пример 14. Вычислить , где область D ограничена окружностями r = а, r = 2 а cosj и лежит вне первой окружности (рис. 29, область АВС).

Область имеет вид, изображенный на рис. 26 (частный случай области А₁А₂В₁В₂, изображенной на рис. 25, точки А₁ и А₂ совпадают, точки В₁ и В₂ – также). Найдем пределы интегрирования. Выясним, в каких границах меняется угол j, для чего определим координаты точек А и В, являющихся точками пересечения данных окружностей. Решая систему уравнений r = а, r = 2 а cosj, находим а = 2 а cosj, откуда , , 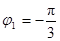. Итак, , .

При фиксированном j из указанного промежутка 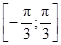r будет меняться от r ₁ = а до r ₂ = 2 а cosj (луч ОЕ, соответствующий данному значению j, пересекает первую окружность в точке D, вторую – в точке Е). Следовательно, r ₁( j ) = а, r ₂( j ) = 2 а cosj.

Таким образом, по формуле (16) получаем

Пример 15. В двойном интеграле 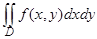, где D ограничена окружностью х² + у² = 1 и прямой х + у = 1, перейти к полярным координатам и расставить пределы интегрирования в том и другом порядке.

Область интегрирования является сегментом круга х² + у² = 1, отсекаемым прямой х + у = 1 (рис. 30). В прямоугольных декартовых координатах данный двойной интеграл сводится к повторному

.

Перейдем к полярным координатам х = r cos j, у = rsinj. Напишем уравнения линий, ограничивающих область D, в полярных координатах. Уравнение окружности х² + у² = 1 перейдет в уравнение r = 1, уравнение прямой х + у = 1 примет вид r(cosj+ sinj) = 1 или 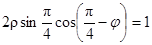, т.е. . Угол j меняется от 0 до 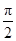. При фиксированном значении угла j соответствующий луч ОВ пересекает границы области в точках А и В (сначала в точке А, принадлежащей прямой, затем в точке В, принадлежащей окружности), т.е. r меняется от до .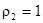

Следовательно, .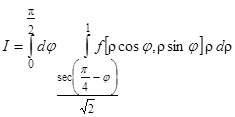

Поменяем порядок интегрирования в данном интеграле. Пределы интегрирования можно установить следующим образом. Зададим такое значение r = r ₀, чтобы окружность радиуса r ₀ проходила внутри области D. Она пересечет хорду сегмента в точках С и D, значения координаты j для которых определяются из уравнения хорды . Полагая в этом уравнении r = r ₀, получаем

, .

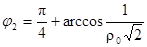Эти значения и являются пределами переменной j во внутреннем интеграле, причем индекс при r можно опустить. Во внешнем интеграле r будет меняться от наименьшего значения , равного длине отрезка ОЕ, до r = 1.

Таким образом,

.

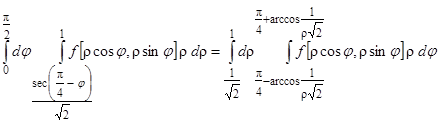Пример 16. Перейдя к полярным координатам, вычислить 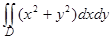, где область D ограничена линиями у = х, 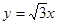и дугой окружности х² + у² = 8, лежащей в первой четверти.

Применим формулы (15), (16), предварительно выразив уравнения границ области и подынтегральную функцию в полярных координатах. Так как х = rcosj, у = rsinj, то уравнения границ области будут:

;

;

.

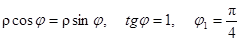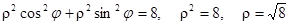Подынтегральная функция 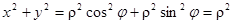; вместо dxdy нужно подставить r d r d j:

Замечание 8. Вычисление данного интеграла в прямоугольных координатах сопряжено с гораздо большим объемом вычислительной работы.

Пример 17. Перейдя к полярным координатам, вычислить 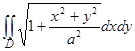, где область D ограничена линиями , (x > 0, y < x).

Область интегрирования ограничена дугой лемнискаты Бернулли и отрезком прямой у = х (см. рис. 31, область ОАВ).

Границы области в полярных координатах х = rcosj, у = rsinj:

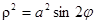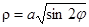, , tgj = 1;

пределы интегрирования: ;

подынтегральная функция .

По формуле (16) получаем

.

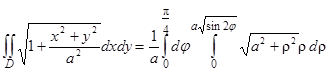Вычислим внутренний интеграл:

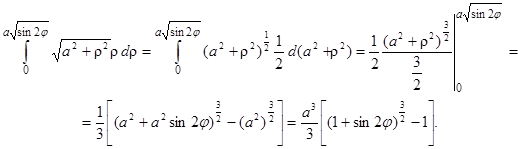
Так как 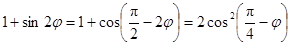, то

,

поэтому

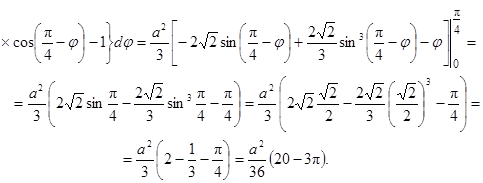
Следовательно, .

Пример 18. В двойном интеграле 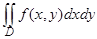, где область D ограничена линиями х = 0, у = 0, х + у = 2, перейти к новым переменным u, v по формулам:

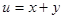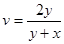, . (17)

Найдем функции j ₁(u, v), y ₁(u, v), определенные формулами (13), т.е. выразим из уравнений (17) х и у через u, v:

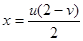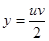, . (18)

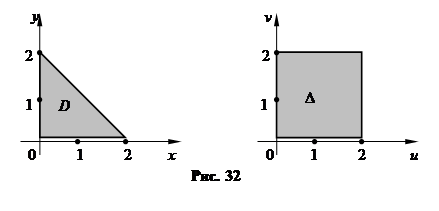
Область D плоскости Оху при преобразовании (18) перейдет в некоторую область D плоскости Ouv, границы которой будут: u = 0, u = 2, v = 0, v = 2. Эти равенства получены из уравнений х = 0, у = 0, х + у = 2 и формул (18). Действительно, если х = 0, то u (2 – v) = 0, откуда u = 0, v = 2; если у = 0, то u = 0, v = 0; если х + у = 2, то u = x + y = 2, u = 2. Область D в плоскости Ouv является прямоугольником (рис. 32).

Найдем выражение для якобиана преобразования (18). Так как

, , , ,

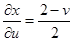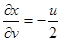то .

Таким образом, в соответствии с формулой (14)

,

где .

Пример 19. В двойном интеграле , где область D – квадрат, ограниченный прямыми х + у = 1, х - у = 1, х + у = 3, х - у = -1 (рис. 33).

		Рис. 33		Рис. 34

Полагаем x+ y = u, x – y = v, откуда , . Тогда якобиан преобразования

, т.е. .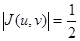

Следовательно, 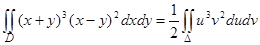. Так как область D также является квадратом (рис. 34), то

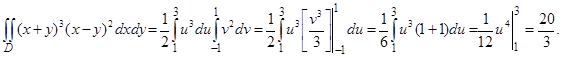
Дата добавления: 2015-06-04