В случае криволинейной области

Приведение двойного интеграла к повторному

Различают два основных вида области интегрирования:

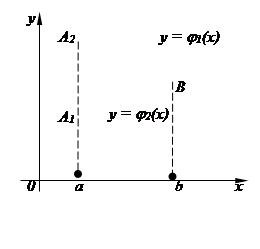
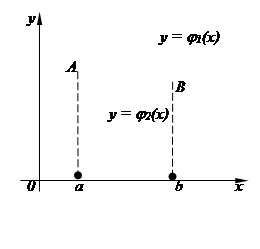
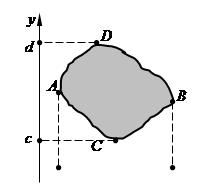
1. Область первого типа D, т.е. область А₁А₂В₂В₁, ограниченную слева и справа прямыми x = a, x = b (a < b) соответственно, снизу – кривой у = j₁(х), сверху – кривой у = j₂(х) [ j₂(х) ³ j₁(х) ], каждая из которых пересекается с вертикалью х = a (a £ a £ b) только в одной точке (рис. 9);

Рис. 10

2. Область второго вида D, т.е. область C₁D₁D₂C₂, ограниченную снизу и сверху прямыми у = с, y = d соответственно, слева – кривой х = y₁(у), справа – кривой х = y₂(у) [ y₂(y) ³ y₁(y) ], каждая из которых пересекается с горизонталью у = b (с £ b £ d) только в одной точке (рис. 10).

Замечание 1. В некоторых случаях точки А₁ и А₂, В₁ и В₂, С₁ и С₂, D₁ и D₂ могут сливаться в одну (см. рис. 11 и рис. 12).

Рис. 11

Рис. 12

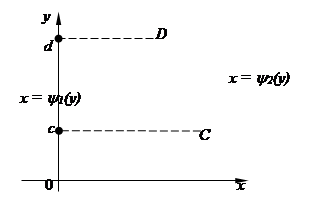Если для функции f(x, y), определенной в области D первого типа, существует двойной интеграл, а при каждом постоянном значении х из [ a, b ] простой интеграл

,

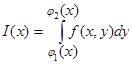то существует также и повторный интеграл

(9)

и выполняется равенство

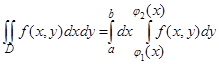. (10)

В случае области второго типа D

(11)

в предположении, что наряду с двойным интегралом существует простой интеграл по х при постоянном у.

Если область D можно рассматривать как область первого вида и как область второго вида (см. рис. 13), то при выполнении указанных условий применимы обе формулы (10) и (11), поэтому

.

0 a b x

	Рис. 13

y

y

Если область интегрирования не принадлежит к рассмотренным выше видам, ее стараются разбить на части, каждая из которых относится к одному из этих видов (рис. 14). Тогда двойной интеграл, в соответствии со свойством 5, равен сумме двойных интегралов.

Замечание 2. В повторном интеграле (9) интегрирование производится сначала по у, при этом х считается постоянным; пределы интегрирования j₁(х) и j₂(х) представляют собой правые части уравнений линий у = j₁(х) и у = j₂(х), ограничивающих область D снизу и сверху соответственно. Другими словами, j₁(х) – это значение ординаты у, при котором прямая х = a «входит» в данную область D, j₂(х) – значение ординаты у, при котором эта прямая «выходит» из указанной области (см. рис. 9). В результате интегрирования получается функция от х, которую потом интегрируют по х в постоянных пределах а и b, являющихся правыми частями уравнений прямых х = а и x = b, ограничивающих область D слева и справа соответственно.

Замечание 3. В повторном интеграле (11) интегрирование производится сначала по х от y₁(у) до y₂(у), при этом у считается постоянным, затем полученную функцию от у интегрируют по у в пределах от с до d (линии х = y₁(у), х = y₂(у); прямые у = с, y = d ограничивают область D; y₁(у) – это «х входа» прямой у = b в области D, y₂(у) – «х выхода» из нее (см. рис. 10)).

Замечание 4. В повторном интеграле (10) нижний предел интегрирования по х равен наименьшей абсциссе точки граница области D (см. рис. 9), верхний предел b равен наибольшей абсциссе точки границы области D.

Замечание 5. В повторном интеграле (11) постоянные пределы интегрирования с и d являются наименьшей и наибольшей ординатами точек границы области D (см. рис. 10).

Пример 7. Вычислить повторный интеграл 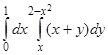. Написать уравнения линий, ограничивающих область интегрирования соответствующего двойного интеграла.

Напишем уравнения линий, ограничивающих область интегрирования. В соответствии с замечанием 2 имеем: х = 0, х = 1 – уравнения прямых, ограничивающих область интегрирования слева и справа; у = х, у = 2 – х² – уравнения линий, ограничивающих эту область снизу и сверху (рис. 15).

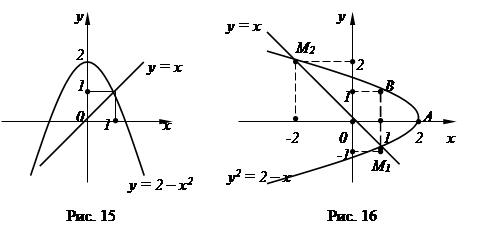Переходим к вычислению повторного интеграла. Вычислим внутренний интеграл, считая х постоянным:

Следовательно,

.

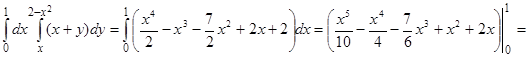
Пример 8. Расставить пределы интегрирования в повторном интеграле, к которому сводится двойной интеграл

,

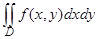где D – область, ограниченная линиями у² = 2 – х, х + у = 0; f(x, y) – функция непрерывная в данной области.

Построим область D (рис. 16). Первая линия – парабола, симметричная относительно оси Ох с вершиной в точке А (2, 0); вторая линия – прямая, проходящая через начало координат (биссектриса второго и четвертого координатных углов). Найдем точки пересечения этих линий. Решая систему уравнений у² = 2 – х и х + у = 0, находим: х₁ = 1, у₁ = -1, х₂ = -2, у₂ = 2; получены точки М₁ (1, -1), М₂ (-2, 2). Область интегрирования является областью второго вида (см. рис. 10). В данном случае х = y₁(у) = -у (найдено из уравнения линии у + х = 0, ограничивающей область слева) и х = y₂(у) = 2 – у² (найдено из уравнения линии у² = 2 – х, ограничивающей область справа), с = -1, d = 2 (наименьшая и наибольшая ординаты точек границы области; см. замечание 5). Следовательно, в соответствии с формулой (11)

.

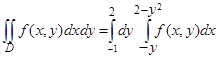Область D можно рассматривать также как сумму двух областей АВМ₁ и М₁ВМ₂ (см. рис. 16), так как линия, ограничивающая снизу криволинейную фигуру АВМ₂М₁А, на различных промежутках определяется различными уравнениями, а именно: если , то у = -х; если , то 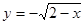. Сверху криволинейная фигура АВМ₂М₁А ограничена кривой 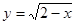. Итак, с другой стороны,

.

Таким образом,

.

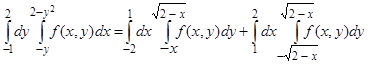Замечание 6. Последняя формула определяет перемену порядка интегрирования в заданном интеграле.

Пример 9. Переменить порядок интегрирования в повторном интеграле , f(x, y) – функция, непрерывная в данной области.

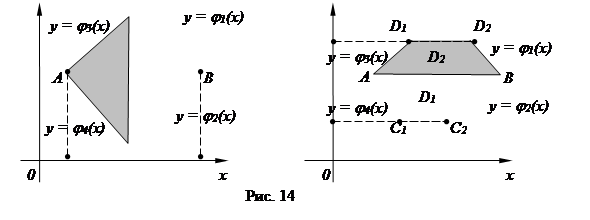
Область интегрирования ограничена линиями у³ = х², у = 2 – х² (рис. 17), пересекающихся в точках М₁ (-1, 1), М₂ (1, 1), т.е. представляет собой криволинейную фигуру 0М₁АМ₂, где А (0, 2) – точка пересечения параболы у = 2 – х² с осью Оу. Эта область является областью первого вида D (см. рис. 9). Ее можно рассматривать также как сумму областей второго типа D₁ и D₂ (см. рис. 14), т.е. областей 0М₁М₂ и М₁АМ₂ (см. рис. 17). Область D₁ ограничена слева дугой 0М₁ графика функции х = y₁(у) = -у^3/2 (получено из уравнения у³ = х²) и справа – дугой 0М₂ графика функции х = y₂(у) =-у^3/2 (получено из того же уравнения) при любом фиксированном у из промежутка [0, 1]. Область D₂ при любом у из [1, 2] ограничена слева дугой М₁А, справа – дугой АМ₂, т.е. дугами графиков функций и соответственно (эти уравнения получены из уравнения у = 2 – х²).

Следовательно, в соответствии со свойством 5

.

Пример 10. Переменить порядок интегрирования в повторном интеграле , f(x, y) – функция, непрерывная в данной области.

Примеры для самостоятельной работы.

1. Найти первые четыре члена ряда .

Дата добавления: 2015-06-04