Основные понятия. Учебно-методическое пособие

Двойной интеграл

Учебно-методическое пособие

КУРСОВОЙ И ДИПЛОМНОЙ РАБОТЫ

СТАНДАРТЫ И ПРАВИЛА ОФОРМЛЕНИЯ

Екатерина Константиновна Рудакова

Наталия Алексеевна Кузнецова

II.4. Диссертационные исследования.

II.3. Справочные издания.

II.2. Статьи.

II.1. Монографии.

II. Литература

Документы международных организаций.

I.4. Документы партий и общественных организаций.

1. Баришпол И.Ф. О роли общественного экологического движения в решении проблем охраны природы // Доклад Председателя президиума ЦС ВООП на II Всероссийском съезде охраны природы 9 февраля 2000 г. [Электронный ресурс]. Режим доступа: http://www.ecocom.ru/archiv/ecocom/2thCongress.

1. Резолюция Генеральной Ассамблеей ООН «Об утверждении Конвенции о предупреждении преступления геноцида и наказания за него» // [Электронный ресурс]. Режим доступа: www.un.org.

1. Акимова Т.А. Экология. М., 1999. С. 256.

1. Адамов Е. Запад в своих требованиях закрыть АЭС в бывшем СССР руководствуется политическими, а не техническими соображениями // Прайм-тасс. 2000. 24 октября.

1. Акты археографической экспедиции 1880 г. М., 2001. Т. 1. № 211. С. 201.

1. Худоренко Е.А. Политическая трансформация современных экологических движений: сравнительный анализ западноевропейского и российского опыта: Диссертация на соискание кандидата политических наук: 23.00.02. М., 2002. С. 123.

ü Обратите внимание. В библиографическом списке нет раздела «Материалы сети Интернет». Следовательно, найденные в сети источники и литературу, необходимо расположить в соответствующих разделах (из перечисленных выше), с указанием данных об авторе, названии публикации, издании.

Пример оформления публикации из Интернет:
Данная публикация является статьей из периодического издания, т.е. должна быть размещена в разделе «Статьи».	Царегородцева И. Турция и Армения угрожают США // Ежедневная деловая газета RBK-daily. 2008. 22 сентября. [Электронный ресурс]. Режим доступа: http://www.rbcdaily.ru/ 2008/09/22/focus/381350.

Факультет международных отношений, экономики и управления

Кафедра международных отношений и политологии

Редактор: Л.П. Шахрова

Лицензия ПД № 18-0062 от 20.12.2010

Подписано к печати Формат 60×84 1/16

Печат.л. Тираж Экз.

Цена договорная

Типография НГЛУ им. Н.А. Добролюбова

603155, Н.Новгород, ул. Минина, 31А

Рассмотрим непустое множество Е точек некоторой плоскости.

Открытый круг радиуса e с центром в точке М (т.е. совокупность всех точек плоскости, расстояния которых до точки М меньше e) называется e -окрестностью или просто окрестностью точки М.

Точка М называется предельной для множества Е, если любая ее окрестность содержит бесконечное множество точек, принадлежащих Е. Предельная точка множества Е может или принадлежать, или не принадлежать этому множеству.

Множество Е называется связным, если при любом его разбиении на два непустых множества Е₁ и Е₂ по крайней мере одно из них содержит предельную точку другого. Если для каждой точки множества Е существует окрестность, все точки которой принадлежат этому множеству, то оно называется открытым.

у 2     -2

у 2   -2

Открытое и связное множество называется областью. Примером области может служить множество всех точек, лежащих внутри некоторого круга (точки ограничивающей его окружности исключаются) или вся плоскость. Например, совокупность точек, координаты которых удовлетворяют условию 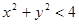, есть область (рис. 1). Множество, состоящее из двух открытых кругов 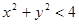и не является областью: оно открыто, но не связано (рис. 2).

Рис. 2

Рис. 1

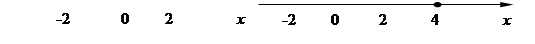Открытое множество является областью тогда и только тогда, когда любые две точки его можно соединить непрерывной линией целиком принадлежащей данному множеству.

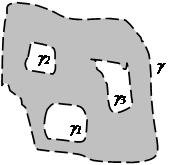
Точка М называется граничной для множества Е, если любая ее окрестность содержит точки, как принадлежащие, так и не принадлежащие множеству Е. Сама граничная точка может или принадлежать, или не принадлежать множеству Е. В частности, открытое множество не содержит ни одной своей граничной точки. Совокупность всех граничных точек множества называется его границей. Множество, содержащее все свои граничные точки, называется замкнутым. Присоединив к некоторой области G все ее граничные точки, получим множество, называемое замкнутой областью . Множество называется ограниченным, если его можно поместить внутрь некоторого круга достаточно большого радиуса.

у

Ограниченная область G называется односвязной или многосвязной в зависимости от того, является ли ее граница связным или несвязным множеством. Множество точек, лежащих внутри круга радиуса R, является простейшим примером односвязной области. Множество точек, лежащих между двумя концентрическими окружностями радиусов R₁ и R₂ – круговое кольцо (точки окружностей исключены), - пример многосвязной области. Эта область называется двусвязной. Граница этой области состоит из двух окружностей радиусов R₁ и R₂ (рис. 3). Если внутри некоторой области G выделить n – 1 (n > 0) замкнутых областей G₁, G₂, …, G_n-1, попарно не имеющих общих точек, то множество всех точек исходной области G, не принадлежащих ни одной из указанных областей, представляет собой n -связную область. Ее граница состоит из n линий: линии g, ограничивающей область G, и линий g_k, ограничивающих области G_k (k = 1, 2, 3, …, n – 1; (на рис. 4 изображена четырехсвязная область).

		Рис. 3		Рис. 4

Пусть Е – ограниченное множество. Расстояние между двумя его произвольными точками М₁ и М₂ обозначим через r (М₁, М₂). Представим, что точки М₁ и М₂, независимо друг от друга, пробегают все множества Е. Очевидно, множество всевозможных расстояний r (М₁, М₂) ограничено сверху (расстояние не может быть больше диаметра круга, в котором помещается множество Е).

Точная верхняя грань чисел r (М₁, М₂) называется диаметром d(E) множества Е (см. рис. 5; диаметром здесь является наибольшая хорда данного множества).

Плоской фигурой называется некоторое ограниченное множество точек плоскости. Аналогично определяются понятия области и фигуры в пространстве. (В этом случае e -окрестностью точки М называются открытый шар радиуса e с центром в точке М.)

	d(E)
		Рис. 5

Дата добавления: 2015-06-04