Решение графо-аналитическим методом с применением геометрических соотношений

Решение методом проекций

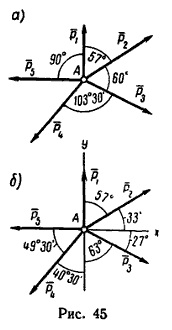
1. Так как силы P₁ и P₅ направлены друг к другу под прямым углом, то и совместим с этими силами ось проекций. Тогда векторы P₂, P₃ и ₄ будут образовывать с осями проекций углы, показанные на рис. 45, б.

2. Найдем проекцию равнодействующей на ось х:
X_R = P₂ cos 33° + P₃ cos 27° - P₄ cos 49°30' - P₅ = 70 cos 33° + 69 cos 27° - 77 cos 49°30' - 70 = 58,6 + 61,4 - 50 - 70 = 0.

3. Найдем проекцию равнодействующей на ось у:
Y_R = P₁ + P₂ sin 33° - P₃ sin 27° - P₄ sin 49°30' = 52 + 70 sin 33° - 69 sin 27° - 77 sin 49°30' = 52 + 38 - 31,4 - 58,6 = 0.

4. Обе проекции искомой равнодействующей равны нулю, значит и сама равнодействующая также равна нулю.

Таким образом, данная система сил уравновешена. Иными словами, любую из пяти заданных сил можно рассматривать как уравновешивающую четыре остальных.

Условие задачи Фонарь весом 9 кГ подвешен на кронштейне ABC (рис. 48, а). Определить реакции горизонтального стержня АВ и наклонной тяги ВС, если AB=1,2 м и BC=1,5 м; крепления в точках А, В и С шарнирные. << задача 36 || задача 40 >>

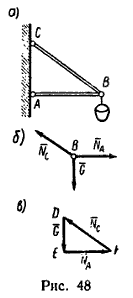
1. В данном случае на шарнир В действуют три силы: вес фонаря G (рис. 48, б) и реакции стержней N_A и N_C, направленные вдоль стержней. Заметим, что стержень АВ сжат, значит реакция N_A направлена от стержня к шарниру, а стержень ВС растянут, поэтому реакция N_Cнаправлена от шарнира к стержню. Шарнир В с действующими на него силами изобразим отдельно.

2. Так как шарнир В под действием этих трех сил находится в равновесии, силовой треугольник, составленный из них, должен быть замкнутым.

Выберем произвольную точку D (рис. 48, в) и отложим от нее отрезок DE, изображающий силу G. Из точек Е и D проведем прямые EF и DF, параллельные соответственно АВ и СВ. В полученном треугольнике DEF сторона EF изображает реакцию N_A (реакцию стержня АВ) и сторона FD – реакцию N_C (реакцию стержня ВС)*.

3. Так как в условии задачи даны линейные размеры кронштейна, величины сил N_A и N_C наиболее просто определить исходя из подобия треугольников ABC и EFD:
BC/N_C = BA/N_A = AC/G.

Отсюда
N_C = G*BC/AC и N_A = G*BA/AC.

4. Неизвестную в задаче длину АС определяем по теореме Пифагора:
AC = sqrt(BC² - BA²) = sqrt(1,5² - 1,2²) = 0,9 м.

5. Окончательно
N_C = 9*1,5/0,9 = 15 кГ и N_A = 9*1,2/0,9 = 12 кГ.

* Если все указанные в п. 2 построения выполнить в определенном масштабе, а затем измеренные длины EF и FD умножить на масштаб построения, то получим решение задачи графическим методом.

Условие задачи В точке В кронштейна ABC (рис. 49, а) подвешен груз M массой 816 кг. Определить реакции стержней кронштейна, если углы кронштейна α=110°, β=30° и крепления в точках А, В и С шарнирные.

Как видно, ответ получается тот же.

После решения задач, аналогичных 39 и 40, можно сделать ошибочный вывод, что силовой треугольник и треугольник, образованный стержнями кронштейна, должны быть подобными. Но это совсем не обязательно. В этом легко убедиться, рассмотрев следующую задачу.

Условие задачи К шарниру В кронштейна ABC прикреплена веревка, перекинутая через блок, к другому концу которой прикреплен груз весом G=1,5 кн (рис. 51, а). Определить усилия в стержнях АВ и СВ кронштейна, если крепления в точках А и С шарнирные, α=35° и β=100°.

Как и следовало ожидать, оба решения дают одинаковый результат. Реакции стержней (их действия на шарнирный болт В) равны N_A=2,57 кн и N_C=1,85 кн. Точно с такими же усилиями действует шарнирный болт на стержни. Стержень АВ растянут силой 2,57 кн, а стержень СВ сжат силой 1,85 кн.

В связи с решением подобных задач методом проекций необходимо отметить следующее. Применяя метод проекций к определению равнодействующей любого числа сходящихся сил, наиболее удобно использовать обычную прямоугольную систему координатных осей. При этом найденные проекции равнодействующей и искомая равнодействующая образуют прямоугольный треугольник, решая который легко определить модуль и направление равнодействующей.

Применяя метод проекций к решению задач на равновесие сил, совсем не обязательно использовать взаимно перпендикулярные оси.

В тех случаях, когда определяются модули сил, направления которых заданы (как в задачах 40 или 41), каждую из осей целесообразно расположить перпендикулярно к направлению искомых сил. Тогда в каждое уравнение равновесия войдет только одно неизвестное.

Дата добавления: 2015-06-04