Состояния с n бозе-частицами

Распространим наш результат на тот случай, когда имеются n частиц. Вообразим случай, изображенный на фиг. 2.4.

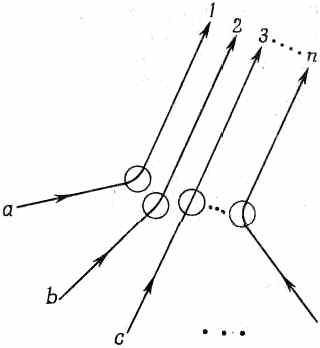
Фиг. 2.4. Рассеяние n частиц в близкие конечные состояния.

Есть n частиц а, b, с,..., которые рассеиваются в направлениях 1, 2, 3,..., п. Все n направлений смотрят в небольшой счет­чик, который стоит где-то поодаль. Как и в предыдущем параг­рафе, выберем нормировку всех амплитуд так, чтобы вероятность того, что каждая частица, действуя по отдельности, попадет в элемент поверхности dS счет­чика, была равна

|< > | ² dS.

Сперва предположим, что частицы все различимы, тогда вероятность того, что n частиц будут одновременно зарегистрированы в n разных элементах поверхности, будет равна

Опять примем, что амплитуды не зависят от того, где в счет­чике расположен элемент dS (он считается малым), и обозна­чим их.просто а, b, с,.... Вероятность (2.15) обратится в

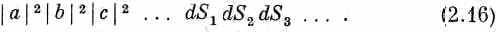
Прогоняя каждый элемент dS по всей поверхности D S счет­чика, получаем, что Р _n(разные) — вероятность одновременно зарегистрировать n разных частиц — равна

Это просто произведение вероятностей попаданий в счетчик каждой из частиц по отдельности. Все они действуют незави­симо — вероятность попасть для одной из них не зависит от того, сколько других туда попало.

Теперь предположим, что все эти частицы — идентичные бозе-частицы. Для каждой совокупности направлений 1, 2, 3,... существует много неразличимых возможностей. Если бы, ска­жем, частиц было только три, появились бы следующие воз­можности:

Возникает шесть различных комбинаций. А если частиц n, то будет n!разных, хотя и не отличимых друг от друга, комбина­ций; их амплитуды положено складывать. Вероятность того, что n частиц будут зарегистрированы в n элементах поверхности, тогда будет равна

│ a ₁ b ₂ c ₃ …+ a₁b₃c₂ … + и т. д. +│² dS ₁ dS ₂ dS ₃... dS_n. (2.18)

И снова мы предположим, что все направления столь близки друг к другу, что можно будет положить а₁=а₂=...... =а_n = а и то же сделать с b, с,...; вероятность (2.18) обратится в

|n! abc... | ² dS ₁ dS ₂ ... dS_n. (2.19)

Когда каждый элемент dS прогоняют по площади D S счет­чика, то всякое мыслимое произведение элементов поверхности считается n!раз; учтем это, разделив на n!, и получим

или

Сравнивая это с (2.17), видим, что вероятность совместного счета n бозе-частиц в n!раз больше, чем получилось бы в пред­положении, что все частицы различимы. Все это можно подыто­жить так:

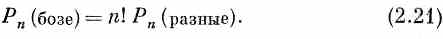
Итак, вероятность в случае бозе-частиц в n!раз больше, чем вы получили бы, считая, что частицы действовали независимо. Мы лучше поймем, что это значит, если спросим: чему равна вероятность того, что бозе-частица перейдет в некоторое состоя­ние, в котором уже находятся n других частиц? Обозначим добавленную частицу буквой w. Если всего, включая w, имеется (n +1) частиц, то (2.20) обращается в

Это можно записать так:

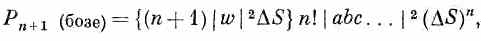
или

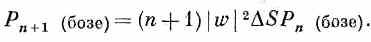
Этот результат можно истолковать следующим образом. Число |w| ²D S — это вероятность заполучить в счетчик части­цу w, если никаких других частиц нет; Р_n (бозе) — это шанс того, что там уже есть n других бозе-частиц. Значит, (2.23) говорит нам, что когда у нас уже есть n других идентичных друг другу бозе-частиц, то вероятность того, что еще одна частица придет в то же состояние, усиливается в (n +1) раз. Вероят­ность получить еще один бозон там, где уже есть их n штук, в (n +1) раз больше той, какая была бы, если бы там раньше ни­чего не было. Наличие других частиц увеличивает вероятность заполучить еще одну.

Дата добавления: 2015-06-04