Излучение и поглощение фотонов

Повсюду в наших рассуждениях шла речь о процессе, по­хожем на рассеяние a-частиц. Но это необязательно; можно было бы говорить и о создании частиц, например об излучении света. При излучении света «создается» фотон. В этом случае уже не нужны на фиг. 2.4 входящие линии; можно просто счи­тать, что есть n атомов а, b, с,..., излучающих свет (фиг. 2.5).

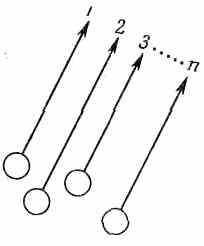
Фиг. 2.5. Образование n фотонов в близких состояниях.

Значит, наш результат можно сформулировать и так: вероятность того, что атом излучит фотон в некотором конечном состоянии, увеличивается в (n+ 1) раз, если в этом состоянии уже есть n фотонов.

Многим больше нравится высказывать этот результат иначе; они говорят, что амплитуда испускания фотона увеличи­вается в Ö(п +1) раз, если уже имеется в наличии n фотонов. Разумеется, это просто другой способ сказать то же самое, если только иметь в виду, что эту амплитуду для получения вероят­ности надо просто возвести в квадрат.

В квантовой механике справедливо в общем случае утвержде­ние о том, что амплитуда получения состояния cиз любого другого состояния j комплексно сопряжена амплитуде получе­ния j из c

Мы разберемся в этом чуть позже, а пока просто предположим, что на самом деле это так. Тогда этим можно воспользоваться, чтобы понять, как фотоны рассеиваются или поглощаются из данного состояния. Мы знаем, что амплитуда того, что фотон прибавится к какому-то состоянию, скажем к i, вкотором уже находится n фотонов, равна

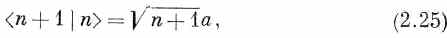
где а =< i| а> — амплитуда, когда нет других фотонов. Если воспользоваться формулой (2.24), то амплитуда обратного перехода — от (n+ 1) фотонов к n фотонам — равна

Но обычно говорят иначе; людям не нравится думать о пере­ходе от (n +1) к n, они всегда предпочитают исходить из того, что имелось n фотонов. Поэтому говорят, что амплитуда погло­щения фотона, если имеется n других, иными словами, перехода от n к (n- 1), равна

<n-1|n>=Öna*. (2.27)

Это, разумеется, просто та же самая формула (2.26). Но тогда возникает новая забота — помнить, когда пишется Ö n и когда Ö(n +1). Запомнить это можно так: множитель всегда равен корню квадратному из наибольшего числа имевшихся в нали­чии фотонов, все равно — до реакции или после. Уравнения (2.25) и (2.26) свидетельствуют о том, что закон на самом деле симметричен; несимметрично он выглядит лишь тогда, когда его записывают в виде (2.27).

Из этих новых правил проистекает множество физических следствий; мы хотим привести одно из них, касающееся испус­кания света. Представим случай, когда фотоны находятся в ящике,— можете вообразить, что ящик имеет зеркальные стен­ки. Пусть в этом ящике в одном и том же состоянии (с одними и теми же частотой, поляризацией и направлением) имеется n фо­тонов, так что их нельзя друг от друга отличить, и пусть в ящике имеется атом, который может испустить еще один фотон в таком же состоянии. Тогда вероятность того, что он испустит фотон, равна

(п+1)| a |², (2.28)

а вероятность того, что он фотон поглотит, равна

n | а |², (2.29)

где | а |² — вероятность того, что он испустил бы фотон, если бы не было этих n фотонов. Мы уже говорили об этих правилах немного по-иному в гл. 42 (вып. 4). Выражение (2.29) утверждает, что вероятность того, что атом поглотит фотон и совершит переход в состояние с более высокой энергией, пропорциональ­на интенсивности света, освещающего его. Но, как впервые указал Эйнштейн, скорость, с которой атом переходит в более низкое энергетическое состояние, состоит из двух частей. Есть вероятность | а| ² того, что он совершит самопроизвольный переход, и есть вероятность вынужденного перехода n|а| ², пропорциональная интенсивности света, т. е. числу имеющихся фотонов. Далее, как заметил Эйнштейн, коэффициенты погло­щения и вынужденного испускания равны между собой и свя­заны с вероятностью самопроизвольного испускания. Здесь же мы выяснили, что если интенсивность света измеряется ко­личеством имеющихся фотонов (вместо того, чтобы пользоваться энергией в единице объема или в секунду), то коэффициенты поглощения, вынужденного испускания и самопроизвольного испускания все равны друг другу. В этом смысл соотношения между коэффициентами А и В, выведенного Эйнштейном [см. гл. 42 (вып. 4), соотношение (42.18)].

Дата добавления: 2015-06-04