Карты материков в азимутальных проекциях

Картографическая сетка в азимутальной проекции строится с помощью картинной плоскости, на которую проецируется поверх­ность глобуса или ее часть. Еще в античной Греции начиная с VI в. до н. э. начали использовать так называемые перспективные проекции. Ученые, разрабатывавшие эти проекции, располагали отличными математическими знаниями и ставили задачу найти про­стые способы перехода от шаровой поверхности к плоскости. Пер­спективные проекции — самые простые в этом отношении. Все точки поверхности земного шара переносятся на касательную к не­му плоскость прямыми лучами. Картографическую сетку в этих проекциях можно получить на основе одних геометрических пост­роений, не прибегая к формулам.

Варианты развертки глобуса могут быть самыми разнообразны­ми и зависят от того, где на поверхности земного шара выбирает­ся точка касания ее плоскостью (рис. 62). Положение точки каса­ния плоскости, в свою очередь, зависит от того, на какую территорию земной поверхности составляется карта. Если точкой касания картинной плоскости и глобуса будет полюс земного ша­ра, то получим картографическую сетку в нормальной азимуталь­ной проекции; если точка касания будет на экваторе, то будет по­строена поперечная азимутальная проекция. В том случае, если точкой касания будет выбрана любая точка, расположенная между полюсом и экватором, то получим картографическую сетку в косой азимутальной проекции. Вид картографических сеток всех вышепе­речисленных проекций будет разным.

В полярной азимутальной проекции на картографической сетке полюс изображается точкой, меридианы — прямыми, отходящими от полюса под углами, равными разности долгот этих меридианов,

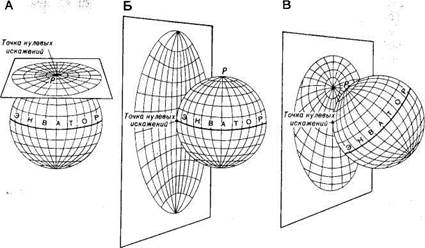
Рис. 62. Образование нормальной (А), поперечной (Б) и косой (В) сеток

азимутальных проекций

а параллели — концентрическими окружностями с центром в по­люсе. Радиусы окружностей вычисляются по определенным форму­лам.

Вид поперечных и косых сеток азимутальных проекций совсем иной, чем у нормальных. Средний меридиан на них — прямая ли­ния, но остальные меридианы — кривые, выпуклые от среднего. Параллели обычно тоже кривые линии. Экватор в косых сетках представлен кривой линией, в поперечных — прямой, перпендику­лярной к среднему меридиану.

Для карт северного и южного полушарий, как правило, исполь­зуют нормальную азимутальную проекцию Постеля (рис. 63). Меридианы в этой проекции прямые, расходящиеся из полюса, а параллели — концентрические окружности. В этой же проекции обычно строят карты Арктики и Антарктики. Данная проекция рав-нопромежуточная и, следовательно, сохраняет по меридианам глав­ный масштаб длин. Масштаб длин по параллелям на разных широ­тах разный. Точка нулевых искажений всех видов находится в центре полушария, т. е. в полюсе. Здесь масштаб площадей га=1, а искажение углов равно нулю. С удалением от полюса искажения возрастают по направлениям радиусов одинаково во все стороны и изоколы имеют вид окружностей.

С XVI до конца XIX в. для карт восточного и западного полушарий широко применялась поперечная стереографичес­кая проекция, предложенная еще во II в. до н. э. Гиппархом (рис. 64). Она относится к так называемым перспективным ази­мутальным проекциям. Меридианы и параллели — дуги эксцентричес­ких окружностей. Центры меридианов лежат на экваторе, а парал-

Рис. 63. Карта Антарктиды в нормальной азимутальной проекции Постеля с изо-колами масштаба площадей и наибольшего искажения углов со. Главный масштаб

1:150 000 000

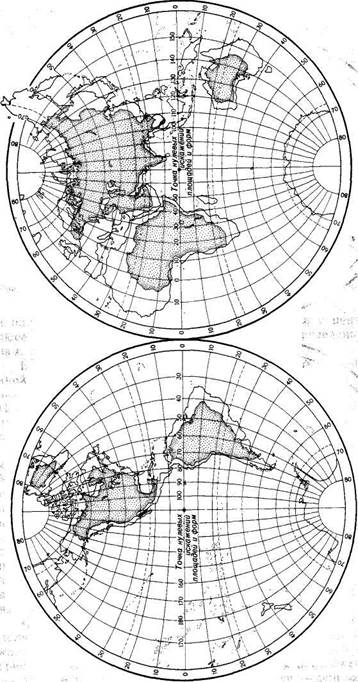
лелей — на среднем меридиане. Расстояния между соседними па­раллелями по среднему меридиану и между меридианами по эк­ватору возрастают от центра полушария к его краям почти в два раза.

Основная проекция для карт восточного и западного полушарий — по­перечная азимутальная проекция Ламберта, предложенная в XVIII в. Почти все карты полушарий в нашей стране строятся в этой проекции. Проекция Ламберта равновеликая; точка нулевых искажений находится в центре каждого полушария. С удалением от центра искажения равномерно нарастают, поэтому изоколы имеют вид окружностей. В этой проекции параллели имеют вид кривых, обращенных выпуклостью к экватору. Средний меридиан — пря­мая, а остальные меридианы имеют вид выпуклых от среднего.

Для всех карт материков используют косую азимутальную проекцию Ламберта. Характер и распределение искажений в этой проекции те же, что и в поперечной проекции Ламберта. Но точ­ки нулевых искажений здесь расположены в центре материков. Ме­ридиан, проходящий через центральную точку материка, имеет вид прямой линии. Остальные меридианы и параллели кривые. Рассто­яния между соседними параллелями по среднему меридиану немно­го уменьшаются от средней части материка к северу и югу, а при удалении от среднего меридиана к западу и востоку эти расстояния постепенно увеличиваются. Данная проекция равновеликая. С уда­лением от точки нулевых искажений (в средней части материка) все искажения нарастают во все стороны одинаково, поэтому изоколы являются окружностями, и величины искажений зависят от разме­ра материка.

Дата добавления: 2015-06-04