Дифференциальные уравнения старших порядков

Дифференциальное уравнение 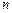-го порядка имеет вид

, ,

или, если оно разрешено относительно ,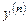

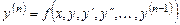. (5.1)

Здесь функция 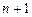переменной 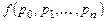определена в некото-рой области ,

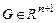а D - область в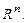

Всякая функция , определенная и 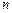раз дифференцируемая на промежутке , называется решением этого уравнения, если она обращает его в тождество при подстановке.

Задача нахождения решения уравнения (5.1), соответству-ющего начальным условиям

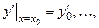
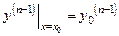(5.2)

называется задачей Коши для уравнения (5.1).

(Здесь )

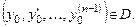Условия (5.2) называются условиями Коши или начальными условиями.

Теорема существования и единственности решения задачи Коши. Если в уравнении (5.1) функция :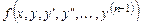

а) непрерывна по всем своим аргументам 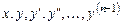в некоторой области G их изменения,

б) имеет ограниченные в области G производные

то найдется интервал 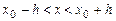, на котором существует единственное решение уравнения (5.1), удовлетворяющее начальным условиям (5.2).

Например, для уравнения второго порядка

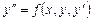
начальные условия имеют вид:

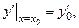
где 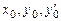- данные числа.

В этом случае теорема существования и единственности утверждает, что через данную точку 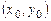с данным угловым коэффициентом касательной 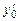проходит единственная интегральная кривая.

Общим решением дифференциального уравнения 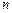-го порядка (5.1) называется множество всех его решений. Оно обычно представляется формулой 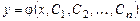, содержащей n произвольных незави-симых между собой постоянных 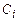, , 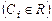таких, что, если заданы начальные условия (5.2), то могут быть найдены все значения , при которых

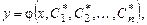
будет частным решением уравнения (5.1), удовлетворяющим условиям (5.2)

В процессе интегрирования уравнения 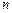- го порядка иногда удается получить уравнение более низкого порядка, эквивалентное исходному. Такое уравнение называется промежуточным интегралом. Промежуточ-ный интеграл 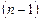-го порядка, т.е. полученный однократным интегри-рованием, называется первым интегралом.

Пример 5.1. .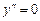

Решение. Покажем, что 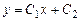удовлетворяет уравнению при любых значениях 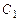и 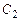. В самом деле,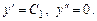

Пусть заданы начальные условия:

.

Покажем, что можно подобрать постоянные 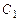и 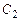, удовлетворяющие начальным условиям. Полагая 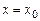, получим систему

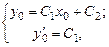
из которой 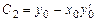. В итоге

,

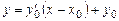частное решение уравнения, удовлетворяющее заданным начальным условиям. Геометрически это означает, что через каждую точку 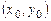плоскости проходит единственная прямая с заданным угловым коэффициентом .

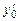Рассмотрим три вида дифференциальных уравнений, допускающих понижение порядка.

1. Уравнение вида 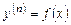. После 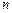-кратного интегрирования получается общее решение

Пример 5.2. .

Решение. Интегрируя последовательно данное уравнение, имеем:

.

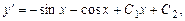
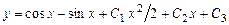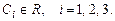
2. Уравнение, не содержащее искомой функции и её производных до порядка включительно:

.

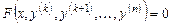Порядок уравнения можно понизить на k единиц заменой

.

Уравнение примет вид:

.

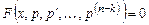Из этого уравнения определяем

, ,

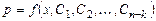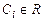а затем из уравнения

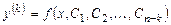
находим y k -кратным интегрированием.

Пример 5.3. .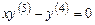

Решение. Полагая 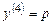, получаем , откуда , .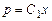

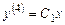Последовательно интегрируя, получаем:

,

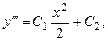
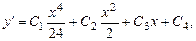
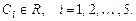
3. Уравнение не содержит независимой переменной:

.

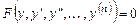Подстановка позволяет понизить прядок уравнения на единицу. Производные 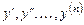выражаются через производные функции .

,

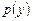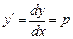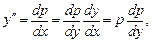
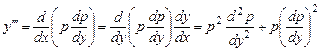и т.д.

Подстановка этих выражений в уравнение приводит к понижению порядка на единицу.

Пример 5.4. .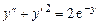

Решение. Уравнение не содержит независимой переменной x. Полагая , ,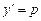

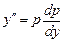получаем уравнение

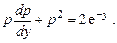
Подстановкой 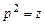оно сводится к линейному уравнению

,

общее решение которого

.

После обратной замены 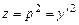имеем

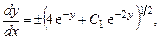
а после разделения переменных

.

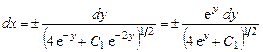Проинтегрировав, получаем

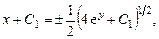
откуда

.

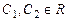Это - общий интеграл данного уравнения.

Б. 4209. .

Решение. Интегрируя уравнение последовательно три раза, получим:

, ,

,

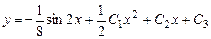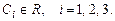
Это - общее решение.

Б. 4163. .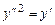

Решение. Уравнение не содержит искомой функции 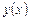, замена переменной позволит понизить порядок уравнения и оно примет вид

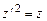или ,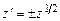

откуда

.

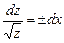
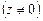Проинтегрировав, получим

, .

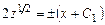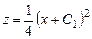Учтем, что 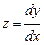, и продолжим интегрирование:

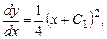
и

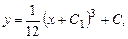C, .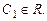

Это - общее решение.

Б. 4171. .

Решение. Уравнение не содержит переменной 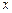. Будем считать 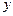независимой переменной, а в качестве искомой функции примем

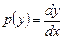, тогда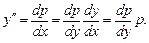

Подставив всё в уравнение, получим:

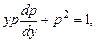откуда .

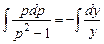После интегрирования:

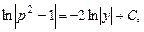
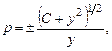
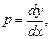
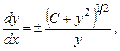
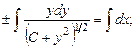
и наконец,

.

Примеры для самостоятельного решения: Б.4157, Б.4166, Б.4177, Б.4183, Б.4190, Б.4213, Б.4214.

Дата добавления: 2015-06-04