
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Системы дифференциальных уравнений
|
|
|
|
Б. 4242.
Б. 4289.
Б. 4281.
Б. 4275 (1-6).
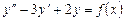 ,
,
где 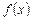 равна:
равна:
1) 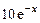 , 2)
, 2) 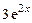 , 3)
, 3) 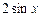 , 4)
, 4) 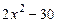 , 5)
, 5) 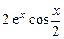 , 6)
, 6) 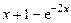 .
.
1. 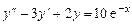 .
.
Решение. Xарактеристическое уравнение 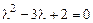 , корни его
, корни его 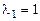 ,
, 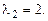 Общее решение однородного уравнения:
Общее решение однородного уравнения:
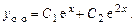
Частное решение неоднородного уравнения ищем в виде 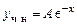 , так как из сопоставления правой части уравнения с формулой (6.10) очевидно, что
, так как из сопоставления правой части уравнения с формулой (6.10) очевидно, что 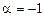 не является корнем характеристического уравнения, т.е. резонанса нет.
не является корнем характеристического уравнения, т.е. резонанса нет.
Подставив 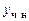 в исходное уравнение, получим
в исходное уравнение, получим
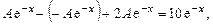
откуда
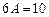 ,
, 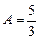 .
.
Общее решение неоднородного уравнения:
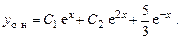
2. 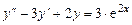 .
.
Решение. Правая часть уравнения имеет вид 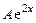 ,
, 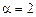 совпадает с корнем характеристического уравнения,
совпадает с корнем характеристического уравнения,  , поэтому вид частного решения неоднородного уравнения
, поэтому вид частного решения неоднородного уравнения  . Найдем А:
. Найдем А:
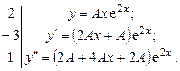
После сложения получим
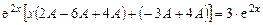 ,
, 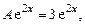
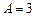 .
.
Общее решение неоднородного уравнения:
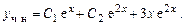
3. 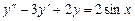 .
.
Решение. Правая часть уравнения имеет вид 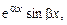
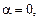
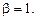 Корни характеристического уравнения не совпадают с числом
Корни характеристического уравнения не совпадают с числом 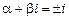 , следовательно резонанса нет и частное решение имеет вид:
, следовательно резонанса нет и частное решение имеет вид:
 .
.
Подставив в уравнение, получим
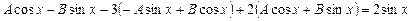 .
.
Приравняв коэффициенты при 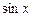 и
и 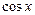 в левой и правой частях равенства, имеем:
в левой и правой частях равенства, имеем:
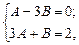 откуда
откуда  ,
, 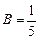 .
.
В итоге общее решение уравнения:
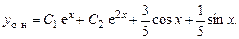
4. 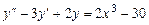 .
.
Решение. Частное решение ищем в виде многочлена с неопределен-ными коэффициентами, степень которого совпадает со степенью многочлена в правой части уравнения:
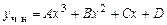 .
.
После подстановки в уравнение получаем
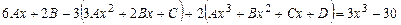 .
.
Приравняв коэффициенты при  и 1 слева и справа, имеем:
и 1 слева и справа, имеем:
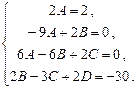
Откуда
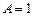 ,
, 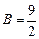 ,
, 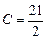 ,
, 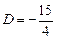 .
.
Общее решение уравнения
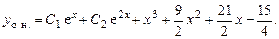
5. 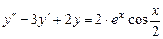 .
.
Решение. Частное решение ищем в виде:
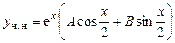 .
.
После подстановки в уравнение получаем:
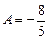 ,
, 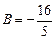 .
.
Общее решение:
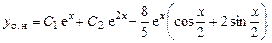
Теорема (принцип суперпозиции или наложения). Если 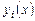 являются решениями уравнений
являются решениями уравнений
 ,
, 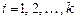 ,
,
то функция
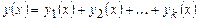
является частным решением уравнения
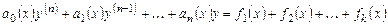 .
.
6. 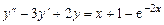 .
.
Правую часть уравнения представим в виде суммы
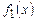 = x + 1 и
= x + 1 и 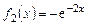
и найдем частные решения 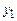 и
и 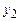 уравнений
уравнений
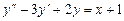 и
и 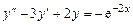 .
.
Методом неопределенных коэффициентов легко получить:
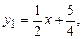
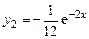 .
.
В соответствии с принципом суперпозиции полагаем, что частное решение уравнения 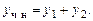
Тогда общее решение исходного уравнения:
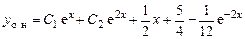 .
.
Решить самостоятельно примеры Б. 4276, Б. 4279.
7. МЕТОД ВАРИАЦИИ ПРОИЗВОЛЬНЫХ ПОСТОЯННЫХ. УРАВНЕНИЕ ЭЙЛЕРА. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С ПЕРЕМЕННЫМИ КОЭФФИЦИЕНТАМИ
Метод вариации постоянныx применим для любого вида неодно-родных линейныx уравнений независимо от вида правой части и позволяет найти общее решение неоднородного уравнения во всех случаях, когда известно общее решение соответствующего однородного уравнения.
Пусть дифференциальное уравнение имеет вид:
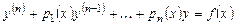 ,
,  (7.1)
(7.1)
а общее решение соответствующего однородного уравнения:

где 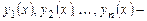 ФСР (7.1).
ФСР (7.1).
Общее решение неоднородного уравнения (7.1) будем искать в виде
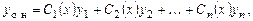 (7.2)
(7.2)
где 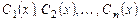 - неизвестные функции, которые определя-ются из следующей системы уравнений:
- неизвестные функции, которые определя-ются из следующей системы уравнений:
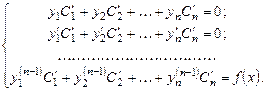
Система уравнений имеет единственное решение, так как её определитель (определитель Вронского)
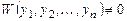 .
.
Решая систему относительно 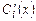 ,
, 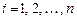 , получаем
, получаем
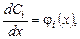
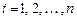 ,
,
откуда
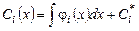 ,
, 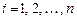 ,
,
где 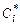 - произвольные постоянные.
- произвольные постоянные.
Подставив найденные функции 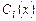 в уравнение (7.2), получим общее решение исходного неоднородного уравнения (7.1).
в уравнение (7.2), получим общее решение исходного неоднородного уравнения (7.1).
Для уравнения второго порядка
 (7.3)
(7.3)
система уравнений имеет вид:
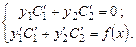
Решая её относительно неизвестных 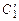 и
и 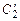 , получим
, получим
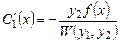 ,
, 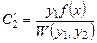 ,
,
откуда находим
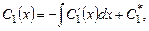
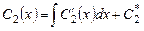 ,
,
подставив которые в уравнение 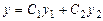 , получим общее реше-ние уравнения (7.3).
, получим общее реше-ние уравнения (7.3).
Пример 7.1.  .
.
Решение. Имеем однородное уравнение - 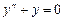 , его характе-ристическое уравнение
, его характе-ристическое уравнение 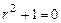 , корни
, корни 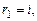
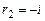 , общее решение однородного уравнения:
, общее решение однородного уравнения:
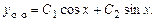
Общее решение исходного неоднородного уравнения ищем в виде
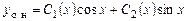 , (7.4)
, (7.4)
где 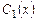 и
и 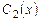 - неизвестные функции.
- неизвестные функции.
Система уравнений для их нахождения имеет вид:
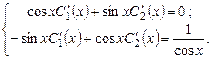
Определитель системы 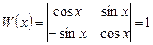 .
.
Система уравнений имеет единственное решение 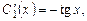
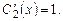 Интегрированием находим
Интегрированием находим
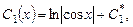
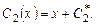
Подставив последние выражения в уравнение (7.4), получаем общее решение исходного неоднородного уравнения:
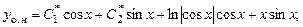
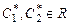
причем 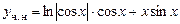 - частное решение исходного урав-нения,.
- частное решение исходного урав-нения,.
Уравнение Эйлера. Уравнение вида
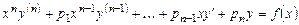 , (7.5)
, (7.5)
где 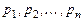 - постоянные, называется уравнением Эйлера. Оно приводится к линейному уравнению с постоянными коэффициентами подстановкой
- постоянные, называется уравнением Эйлера. Оно приводится к линейному уравнению с постоянными коэффициентами подстановкой 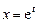
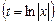 . Считая
. Считая 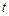 промежуточным аргументом, найдем производные:
промежуточным аргументом, найдем производные:
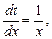
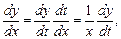
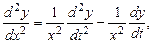
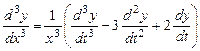 и т.д.
и т.д.
Подстановка производных в уравнение Эйлера превращает его в уравнение с постоянными коэффициентами.
Пример 7.2. 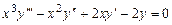 .
.
Решение. Полагая 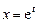 и подставив найденные выше выражения для производных, получим
и подставив найденные выше выражения для производных, получим
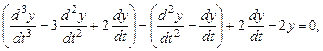
или
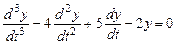 .
.
Его характеристическое уравнение 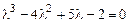 , корни
, корни 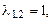
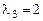 .
.
Общее решение
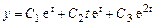 ,
,
или
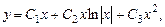
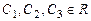 .
.
Заметим, что вид решений уравнения Эйлера 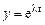 , или в исходных переменных
, или в исходных переменных 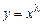 . Поэтому можно искать решения в виде
. Поэтому можно искать решения в виде 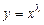 , не производя предварительно замену переменной
, не производя предварительно замену переменной 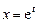 .
.
Пример 7.3.  .
.
Решение ищем в виде 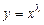 . Подставив это в уравнение, получим
. Подставив это в уравнение, получим
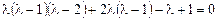 ,
,
или  . Корни уравнения
. Корни уравнения 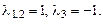 Общее реше-ние:
Общее реше-ние:
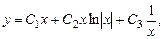
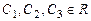 .
.
Здесь очевидно, что корню  кратности
кратности 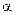 соответствуют
соответствуют 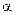 решений
решений
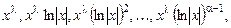
а паре комплексно-сопряженных корней 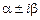 - пара решений
- пара решений
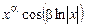 и
и 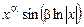 .
.
Неоднородное уравнение Эйлера может быть проинтегрировано методом вариации произвольных постоянных. Для некоторых типов правых частей возможно применение метода неопределенных коэффи-циентов.
Линейные уравнения с переменными коэффициентами. Если известно частное решение 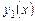 линейного однородного уравнения вида
линейного однородного уравнения вида
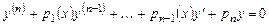 ,(7.6)
,(7.6)
то его порядок можно понизить на единицу при помощи подстановки
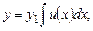 (7.7)
(7.7)
где 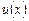 - новая искомая функция. Полученное в результате уравнение также будет линейным.
- новая искомая функция. Полученное в результате уравнение также будет линейным.
Пример 7.4. Доказать, что если 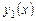 - частное решение линейного однородного уравнения второго порядка
- частное решение линейного однородного уравнения второго порядка
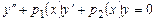 , (7.8)
, (7.8)
то второе его решение, линейно независимое с первым, находится по формуле:
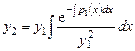 . (7.9)
. (7.9)
Решение. Подставим выражение (7.7) в уравнение (7.8), имея в виду, что 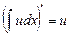 . Получим
. Получим
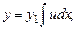
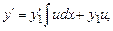
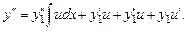
Подставив в уравнение (7.8), найдем
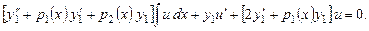
Выражение, стоящее в первых квадратных скобках, есть результат подста-новки решения 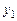 в исходное уравнение, следовательно, равно нулю. Полученное уравнение
в исходное уравнение, следовательно, равно нулю. Полученное уравнение
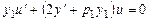 (7.10)
(7.10)
есть линейное однородное первого порядка.
Разделяя переменные, получим
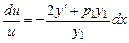 .
.
Проинтегрируем
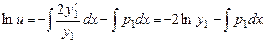 .
.
Откуда
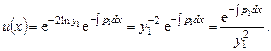
Это - решение уравнения (7.10). Подставив 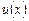 в формулу (7.7), найдем второе решение уравнения (7.8)
в формулу (7.7), найдем второе решение уравнения (7.8)
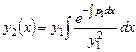 . (7.11)
. (7.11)
Это - формула Остроградского - Лиувилля для уравнения (7.8).
Пример 7.5. 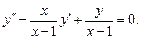
Найти общее решение уравнения, если известно его частное решение 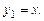
Решение. Здесь 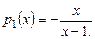 Вычислим входящий в формулу (7.11) интеграл
Вычислим входящий в формулу (7.11) интеграл
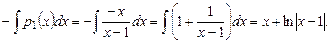
Далее
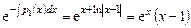 .
.
Подставив все в формулу (7.11), получим решение 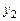 .
.
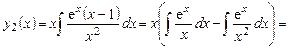

Общее решение уравнения: 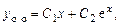
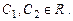
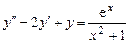 .
.
Решение. Для нахождения общего решения этого неоднородного уравнения применим метод вариации произвольных постоянных.
Общее решение однородного уравнения имеет вид
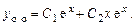
Решение неоднородного уравнения будем искать в виде
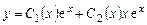 . (7.12)
. (7.12)
Неизвестные функции 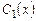 и
и  определим из системы уравнений:
определим из системы уравнений:
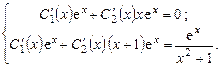
Вычитая первое уравнение из второго, находим
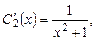 откуда
откуда 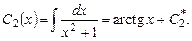
Подставив 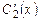 в первое уравнение, получим
в первое уравнение, получим
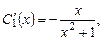
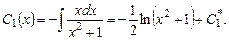
Подставив 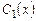 и
и  в выражение (7.12), получим общее решение неоднородного уравнения
в выражение (7.12), получим общее решение неоднородного уравнения
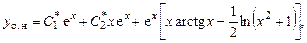 где
где 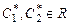 .
.
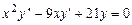 .
.
Решение. Это - уравнение Эйлера. Решение ищем в виде 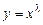 . Подставив в уравнение, получим
. Подставив в уравнение, получим 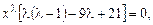 откуда
откуда 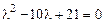 - характеристическое уравнение. Корни его
- характеристическое уравнение. Корни его 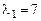 ,
, 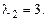 Общее решение
Общее решение
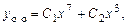
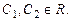
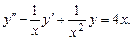
Решение. Однородное уравнение имеет решение 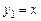 , в чем легко убедиться, подставив его в уравнение. Решение
, в чем легко убедиться, подставив его в уравнение. Решение 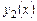 найдем по формуле Остроградского - Лиувилля (7.11), учитывая, что
найдем по формуле Остроградского - Лиувилля (7.11), учитывая, что 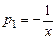
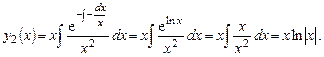
Общее решение однородного уравнения:
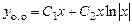 .
.
Общее решение неоднородного уравнения найдем методом вариации про-извольных постоянных в виде
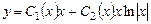 . (7.13)
. (7.13)
Система уравнений для неизвестных функций 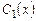 и
и  :
:
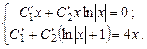
Умножив второе уравнение на x и вычтя из него первое, получим
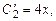
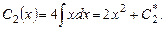
Подставив в первое уравнение 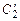 , найдем
, найдем
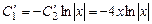 ,
,
откуда
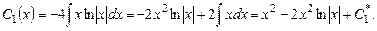
Подставив 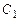 и
и 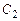 в формулу (7.13), получим общее решение
в формулу (7.13), получим общее решение
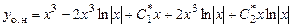 ,
,
или
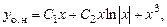
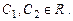
Составление дифференциального уравнения по заданной фунда-ментальной системе решений.
Пусть  - линейно независимые n раз диффе-ренцируемые функции. Тогда уравнение:
- линейно независимые n раз диффе-ренцируемые функции. Тогда уравнение:
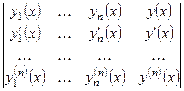 = 0, (14)
= 0, (14)
где 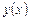 - неизвестная функция, будет линейным дифференциальным уравнением, для которого функции
- неизвестная функция, будет линейным дифференциальным уравнением, для которого функции 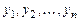 образуют фундамен-тальную систему решений.
образуют фундамен-тальную систему решений.
Пример 7.6. Составить дифференциальное уравнение, для которого 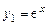 и
и 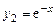 образуют фундаментальную систему решений.
образуют фундаментальную систему решений.
Решение. Составим определитель (7.14).
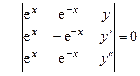 или
или 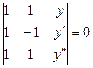 .
.
Раскрывая определитель по элементам третьего столбца, получим искомое дифференциальное уравнение 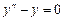 .
.
Б. 4230. Составить дифференциальное уравнение, для которого функ-ции  и
и 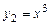 образуют фундаментальную систему решений.
образуют фундаментальную систему решений.
Решение. Составим определитель (7.14)
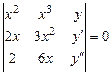 .
.
Раскроем его по элементам третьего столбца.
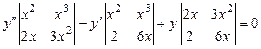 .
.
Вычислив определители второго порядка и отбросив общий множитель 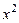 , получим
, получим
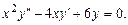
Решить самостоятельно Б. 4228, Б. 4238, Б. 4240, Б. 4243, Б. 4280, Б. 4282, Б. 4290, Б. 4291.
Система обыкновенных дифференциальных уравнений первого порядка вида
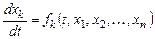 ,
, 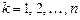 , (8.1)
, (8.1)
где 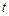 - независимая переменная;
- независимая переменная; 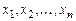 -неизвестные функции пере-менной
-неизвестные функции пере-менной 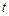 , называется нормальной системой. Считается, что функции
, называется нормальной системой. Считается, что функции 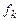 определены в некоторой области D переменных
определены в некоторой области D переменных 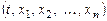 .
.
Число n называется порядком нормальной системы (8.1). Две системы дифференциальных уравнений называются эквивалентными, если они обладают одними и теми же решениями.
Частным решением системы на интервале 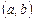 называется совокуп-ность любых n функций
называется совокуп-ность любых n функций
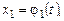
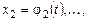
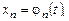
определенных и непрерывно дифференцируемых в интервале 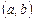 , если они обращают все уравнения системы (8.1) в верные равенства при всех значениях
, если они обращают все уравнения системы (8.1) в верные равенства при всех значениях 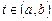 .
.
Задачей Коши для системы (8.1) называется задача нахождения решения
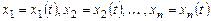 ,
,
удовлетворяющего начальным условиям
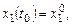
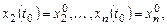 (8.2)
(8.2)
где точка 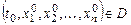 - фиксирована.
- фиксирована.
Теорема существования и единственности решения задачи Коши. Пусть имеется нормальная система дифференциальных уравнений (8.1) и пусть функции 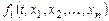
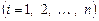 определены в (
определены в (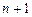 )-мерной области D изменения переменных
)-мерной области D изменения переменных 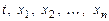 .
.
Если функции 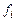 непрерывны и имеют ограниченные частные производные по переменным
непрерывны и имеют ограниченные частные производные по переменным 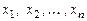 в D, то найдется интервал
в D, то найдется интервал 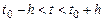 , в котором существует единственное решение системы (8.1), удовлетворяющее начальным условиям (8.2).
, в котором существует единственное решение системы (8.1), удовлетворяющее начальным условиям (8.2).
Система, состоящая из n дифференцируемых функций
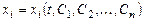 ,
, 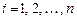 (8.3)
(8.3)
независимой переменной 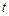 и
и 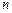 произвольных постоянных
произвольных постоянных 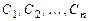 называется общим решением нормальной системы (8.1), если:
называется общим решением нормальной системы (8.1), если:
1) при любых допустимых значениях 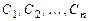 система функций (8.3) обращает уравнения (8.1) в тождества,
система функций (8.3) обращает уравнения (8.1) в тождества,
2) любое частное решение может быть получено соответствующим подбором постоянных 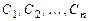 .
.
Нормальная система n уравнений первого порядка
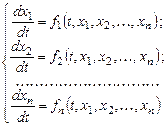
сводится к одному уравнению прядка 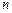 . На этом основан один из методов интегрирования систем дифференциальных уравнений – метод исключения.
. На этом основан один из методов интегрирования систем дифференциальных уравнений – метод исключения.
Метод исключения состоит в следующем. Из уравнений системы и уравнений, получающихся дифференцированием уравнений системы, исключаем все неизвестные функции, кроме одной. Для неё получаем одно ОДУ более высокого порядка. Решая полученное уравнение, определяем одну из функций, а остальные находим без интегрирования, из исходных уравнений и их следствий.
Проиллюстрируем этот метод на примере системы второго порядка.
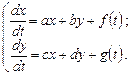 (8.4)
(8.4)
Здесь 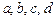 - постоянные;
- постоянные; 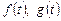 - заданные функции;
- заданные функции; 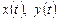 - искомые функции.
- искомые функции.
Из первого уравнения системы (8.4) находим:
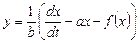 . (8.5)
. (8.5)
Подставив во второе уравнение системы вместо 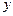 правую часть выражения (8.5), а вместо
правую часть выражения (8.5), а вместо 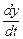 - её производную, получим уравнение второго порядка относительно
- её производную, получим уравнение второго порядка относительно 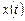 :
:
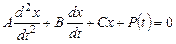 ,
,
где 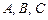 - постоянные. Из этого уравнения находим
- постоянные. Из этого уравнения находим 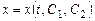 . Подставив
. Подставив 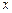 и
и 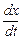 в уравнение (8.5), найдем
в уравнение (8.5), найдем 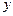 .
.
Пример 8.1. Решить систему уравнений:
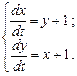 (8.6)
(8.6)
Решение. Из первого уравнения системы (8.6) находим
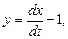
откуда

Подставив это во второе уравнение системы (8.6), получим линейное уравнение с постоянными коэффициентами второго порядка
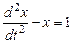 .
.
Его общее решение находим изученными ранее методами:
 .
.
Подставив его производную в выражение для y, получаем
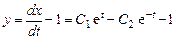 ,
, 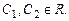
Метод наxождения интегрируемыx комбинаций. Пусть имеется система дифференциальных уравнений:
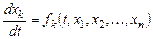 ,
, 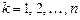 . (8.7)
. (8.7)
Суть метода состоит в том, что с помощью подходящих ариф-метических операций из уравнений системы (8.7) образуются комбинации, которые достаточно просто проинтегрировать.
Каждая комбинация дает один интеграл системы. Если найдены 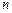 независимых интегралов, то интегрирование системы закончено. Если найдено меньшее число интегралов, то система (8.7) сводится к системе с меньшим числом неизвестных.
независимых интегралов, то интегрирование системы закончено. Если найдено меньшее число интегралов, то система (8.7) сводится к системе с меньшим числом неизвестных.
Пример 8.2. Решить систему уравнений:
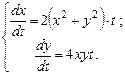 (8.8)
(8.8)
Решение. Складывая оба уравнения, получим
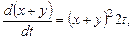
откуда
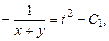
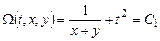 .
.
Вычитая уравнения, получим
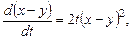

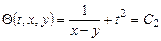 .
.
Интегралы 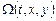 и
и 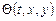 независимы, если определитель Якоби их системы отличен от нуля:
независимы, если определитель Якоби их системы отличен от нуля:
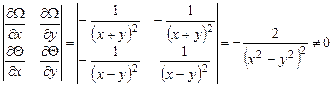 .
.
Общий интеграл системы (8.8)
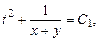
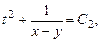
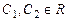 . (8.9)
. (8.9)
Решая систему (8.9) относительно 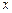 и
и 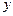 , получим общее решение системы уравнений (8.8).
, получим общее решение системы уравнений (8.8).
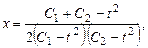
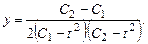
Пример 8.3. Найти частное решение системы:
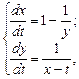
удовлетворяющее начальным условиям 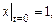
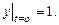
Решение. Запишем данную систему в виде:
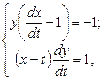 или
или 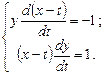
Складывая последние уравнения, получаем
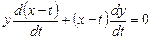 или
или 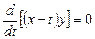 ,
,
откуда
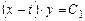 .
.
Подставив 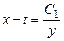 во второе уравнение, найдем
во второе уравнение, найдем
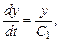 откуда
откуда 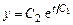 .
.
Выразив 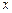 и
и 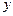 из полученных интегралов, запишем общее решение
из полученных интегралов, запишем общее решение
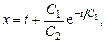
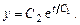 (8.10)
(8.10)
Найдем частное решение, удовлетворяющее начальным условиям; подста-вив 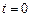 в (8.10), получим
в (8.10), получим
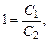
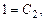 откуда
откуда 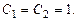
Искомое частное решение:
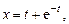
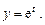
Б. 4324.1. Решить систему уравнений:
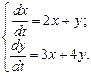
Решение ищем методом исключения, преобразуя систему в уравнение второго порядка. Выразим y из первого уравнения и подставим во второе:
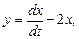
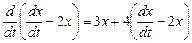 ,
,
или
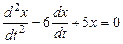 .
.
Характеристическое уравнение:
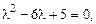 корни
корни 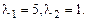
Общее решение:
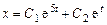 .
.
Подставив найденное в выражение для 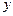 , получим
, получим
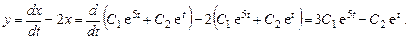
Общее решение системы:
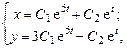
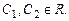
Решить самостоятельно Б. 4324.2, Б. 4324.3, Б. 4324.4, Б. 4326, Б. 4331,
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 738; Нарушение авторских прав?; Мы поможем в написании вашей работы!