Дифференциальных уравнений

МЕТОД ЭЙЛЕРА ИНТЕГРИРОВАНИЯ СИСТЕМ ЛИНЕЙНЫХ

Линейная однородная система с постоянными коэффициентами

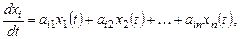
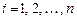
может быть кратко записана в виде матричного уравнения:

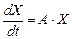, (9.1)

где

, , .

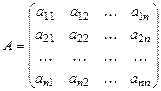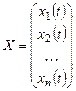Система частных решений

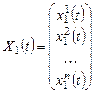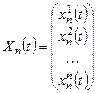, , (9.2)

(здесь нижний индекс указывает номер решения, а верхний - номер функции в решении) называется фундаментальной на интервале 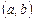, если её определитель Вронского для всех 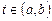не равен нулю.

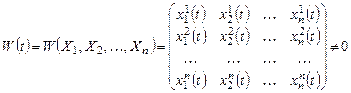
Теорема. Если система частных решений (9.2) линейной однородной системы дифференциальных уравнений является фундаментальной, то общее решение этой системы имеет вид:

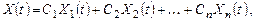
где 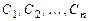- произвольные постоянные.

Метод Эйлера интегрирования систем дифференциальных уравнений рассмотрим на примере системы трех линейных однородных уравнений:

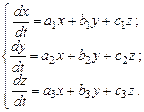(9.3)

Решение системы ищем в виде

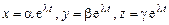. (9.4)

Подставив (9.4) в (9.3), получим систему уравнений для определения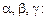

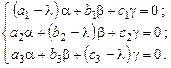(9.5)

Система (9.5) имеет ненулевое решение, если её определитель равен нулю:

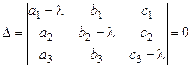(9.6)

Вычисление определителя (9.6) приводит к уравнению третьей степени с вещественными коэффициентами, корни которого могут быть действительными различными, кратными, или комплексными. Матрица (9.6) называется характеристической.

Рассмотрим три случая.

1. Пусть корни уравнения 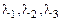- действительные различные.

Подставив 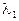в систему (9.5) и решив её, получим числа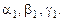

Аналогичным образом, используя корн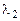и и 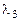, находим наборы чисел 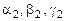и

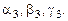
Общее решение системы будет иметь вид:

;

;

.

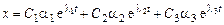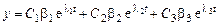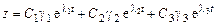В векторной форме

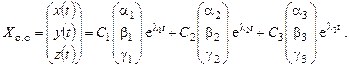
Пример 9.1. Решить систему:

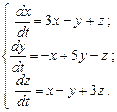(9.7)

Решение ищем в виде 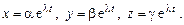Подставив 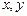и 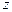в систему (9.7), получаем систему алгебраических уравнений:

(9.8)

Запишем характеристическую матрицу и найдем корни:

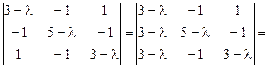
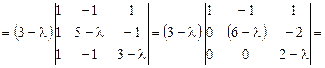
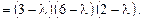
Корни уравнения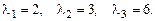

Подставляя корни поочередно в систему (9.8), получаем три набора чисел .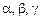

Подставив 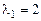в систему (9.8), получим

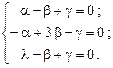
Здесь третье уравнение совпадает с первым и может быть отброшено. (Так и должно быть, поскольку определитель системы уравнений равен нулю.) Сложив оставшиеся уравнения, получим 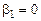, а из первого уравнения получим . Приняв 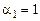, получим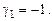

В итоге, подставив все корни и проделав необходимые вычисления, имеем:

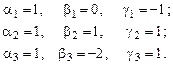
Общее решение в векторной форме:

,

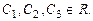
2. Случай кратных корней.

Пример 9.2. Решить систему:

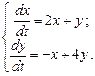(9.9)

Решение ищем в виде 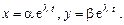Подставив 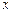и 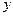в систему (9.9) и сократив 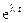, получим систему алгебраических уравнений:

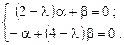
Найдем корни её характеристической матрицы (собственные значения):

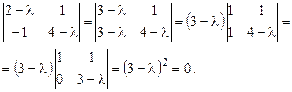
Корень кратности 2,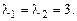

Решение следует искать в виде

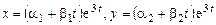. (9.10)

Подставив (9.10) в первое уравнение системы (9.9), получим

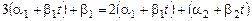. (9.11)

Сравнивая коэффициенты при одинаковых степенях t в левой и правой частях (9.11), получаем

;

,

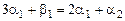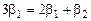откуда

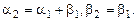
Величины и 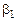остаются произвольными (так как определитель характеристической матрицы равен нулю). Обозначая их соответственно 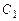и 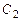, получим общее решение системы:

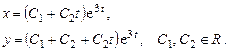
3. Случай комплексных корней.

Пример 9.3. Решить систему:

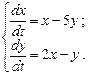(9.12)

Решение. Подставив в систему 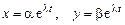, получим

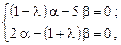
характеристическое уравнение системы (9.12). Детерминант системы

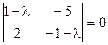
имеет корни

.

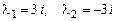Подставляя 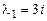в (9.12), получаем два уравнения для определения и :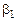

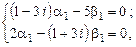
из которых одно является следствием другого (так как определитель системы (9.12) равен нулю).

Возьмем 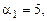тогда 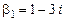и первое частное решение

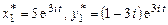
Аналогично, подставляя 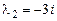в (9.12), найдем второе частное решение:

.

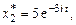
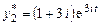Используя формулу Эйлера 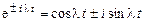, можно пре-образовать систему решений:

;

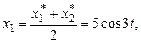
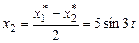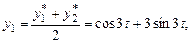
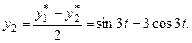
Общее решение системы

,

,

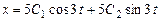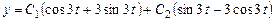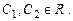
Неоднородные системы линейныx уравнений. Пусть имеется систе-ма неоднородных линейных уравнений с постоянными коэффициентами

,

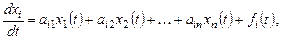
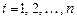или в матричном виде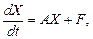

где F - матрица-столбец, элементами которого являются функции .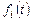

Теорема. Общее решение 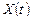неоднородной линейной системы равно сумме общего решения 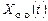соответствующей однородной системы и любого частного решения 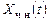данной неоднородной системы:

.

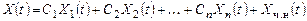Найти частное решение неоднородной системы можно методомвариации произвольных постоянных .

Проиллюстрируем этот метод на примере системы трёх уравнений:

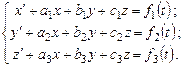(9.13)

Пусть общее решение однородной системы:

;

;

.

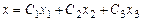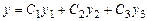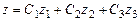Решение неоднородной системы ищем в виде

;

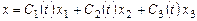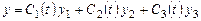; (9.14)

.

Подставив (9.14) в первое уравнение системы (9.13), получим

.

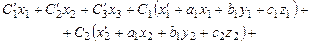
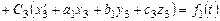Все суммы в скобках обратятся в нуль, так как содержат результаты подстановки решений в уравнение. В итоге:

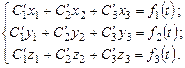(9.15)

Два последних уравнения системы (9.15) получены в результате подстановки системы решений (9.14) во второе и третье уравнения системы (9.13).

Система уравнений (9.15) относительно неизвестных 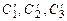имеет решение, так как её определитель отличен от нуля:

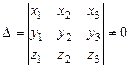
в силу линейной независимости решений однородной системы.

Проинтегрировав 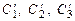, найдем 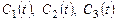, а тем самым и решение неоднородной системы (9.13).

Пример 9.4. Методом вариации постоянных решить систему:

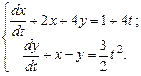(9.16)

Решение. Общее решение соответствующей однородной системы:

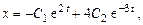
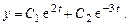
Решение неоднородной системы ищем в виде

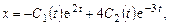
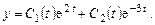(9.17)

Подставив это в систему (9.16), получим

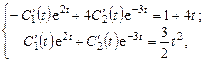
откуда

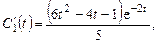
Проинтегрировав, получим

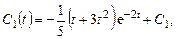
Подставив это в (9.17), получим общее решение неоднородной системы

;

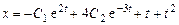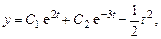
Решить самостоятельно Б.4324, Б. 4326.

ЛИТЕРАТУРА

Дата добавления: 2015-06-04