Спектр енергії для вільної релятивістської частинки

Хвильова функція вільної частинки пропорційна до плоскої хвилі

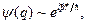
тобто це є стан з певним значенням імпульса і вся його залежність від просторо­вих координат виражається функцією 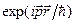. Підстановка цієї функції у рів­нян­­ня Дірака дає

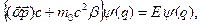
тут 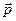– вже є імпульсом частинки, а не оператором .

Надалі зручно виразити чотирьохкомпонентну функцію через дві двохком­по­нент­ні функції

,

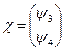
за допомогою співвідношення

Якщо записати стаціонарне рівняння Дірака у вигляді (тобто через двохрядні матриці Паулі)

то безпосередньо видно, що функці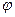ї і 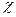задовольняють систему двох матрич­них рівнянь

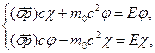
або

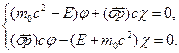
Відмінні від нуля розв’язки цієї системи будуть тільки при рівності нулеві її визначника:

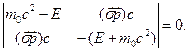
Якщо розкрити цей визначник та скористатися рівністю

яку легко довести, якщо скористатися властивостями матриць Паулі, то знайдемо

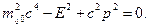
Отже, корені цього рівняння

де

,

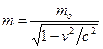– звичний нам вираз енергії релятивістської частинки у теорії відносності.

Ми одержали спектр енергії для вільної релятивістської частинки. Двом знакам у виразі для відповідають два типи розв’язків рівняння Дірака для станів з різним знаком енергії в експоненті, що визначає залежність хвильової функції 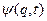від часу:

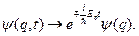
Стани з від’ємною енергією слід розглядати як стани, що описують частинки з додатною енергією, але з протилежним зарядом. До цього висновку приходять при вивченні властивостей симетрії множини розв’язків Дірака. Ми не маємо можливості в наших лекціях детально обговорювати це важливе питання. Скажемо тільки, що у теорії квантованих полів, зокрема в теорії квантованого електронно-позитронного поля, труднощів з від’ємними рівнями енергії немає і вся теорія набуває рис послідовності і чіткості.

Дата добавления: 2015-06-04