Деякі відомості з функціонального аналізу

Математика для квантової механіки

Додаток до лекції

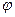Нехай енергія вільної релятивістської частинки , . Із другого рівняння системи двох алгебраїчних лінійних рів­нянь для функцій і 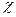у випадку вільної релятивістської частинки знаходимо

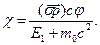
Але

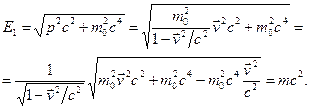
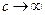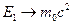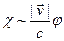У нерелятивістській межі , , а , бо

Висновок. При переході до нерелятивістської теорії при основну роль відіграє функція 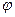, а функція 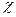є малою.

Математичний додаток

Лінійні простори. До поняття лінійного простору ми приходимо, розгля­даючи загальні властивості елементарних алгебраїчних операцій (додавання і мно­ження на число), з якими ми зустрічаємось у звичайній векторній алгебрі. Лінійним простором називається множина елементів будь-якої природи, для яких визначені операції додавання і множення на число з виконанням звичай­них для цих операцій законів. Елементами лінійного простору можуть бути, наприклад, вектори -вимірного евклідового простору, функції з множини непе­рервних функцій або функціонали. Для абстрактної теорії цих просторів конкретна природа їх елементів неістотна.

Простір 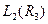функцій 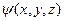. Це клас (множина) комплекснозначних функцій трьох дійсних змінних , для яких

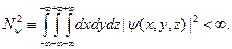
Надалі функції будемо називати векторами простору 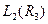. Вико­ристовуватимемо позначення , , , .

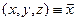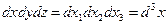Скалярний добуток у просторі 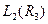. Нехай 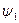і 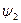– два вектори простору 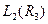. За означенням

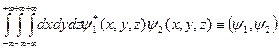
це скалярний добуток вектора 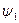на вектор 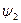. Надалі дуже зручно функцію 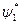називати со-вектором вектора 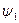, а наведений вище вираз читати як скалярний добуток со-вектора вектора 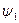на вектор 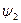і позначати його сим­волом .

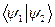Простір 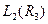– унітарний векторний простір. У цьому просторі є конкретно визначений скалярний добуток для кожної пари векторів із .

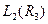Норма вектора простору 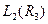. Число 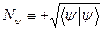за означенням є нормою вектора 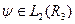. Коротко норму вектора 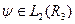позначають симво­лом 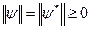. Якщо , тоді вектор – це так званий «нульовий» вектор в просторі 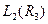. Отже, простір 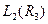слід вважати нормованим.

Відстань між двома векторами простору 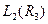. Для кожної пари 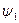, 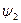із 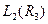є визначене дійсне число

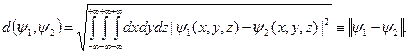
Число задає відстань між векторами 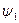, 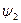із .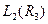

Простір 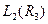– повний нормований векторний простір. Дійсно, адже 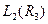нормований векторний простір, а це означає, що він є метричним з метрикою . Отже, в ньому мож­на дослідити питання про збіжність будь-якої фунда­ментальної послідовності векторів простору 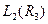. Існує теорема: кожна послідовність векторів простору 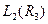, яка задовольняє умову

,

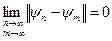тобто є послідовністю Коші, збігається до деякого вектора 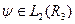. Через це простір 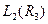називають повним нормованим векторним простором. У матема­тиці повні унітарні векторні простори називають Ґільбертовими просторами.

Абстрактний простір Ґільберта. Досі ми мали конкретну реалізацію простору Ґільберта, коли роль векторів грали функції 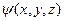. Але таку роль можуть грати елементи множини будь-якої іншої природи. Наприклад, це мо­жуть бути множини матриць, множини скінченновимірних векторів, тощо. Че­рез це в подальшому для позначення векторів Ґільбертового проснору вико­ристовуватимемо два символи: 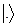та 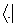. На місці крапки всередині цих символів писатимемо «регалії» (тобто, значки), які відрізняють один вектор від іншого.

Якщо використаємо запропоновані символи для того, щоб модернізувати позначення векторів простору 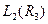, то будемо їх представляти у вигляді 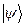та 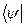. Скалярний добуток вектора на вектор 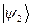позначатимемо символом 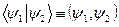. Такі позначення вперше запропонував Дірак.

Простір 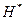спряжений до простору Ґільберта. Можна привести яскравий приклад лінійного функціонала 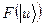в Ґільбертовому просторі 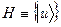– це скалярний добуток на довільно фіксованому векторі :

,

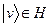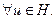
Можна довести, що функціонали цього типу вичерпують всі лінійні (неперерв­ні) функціонали (теорема Рисса). Це означає, що простір 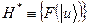ізоморф­ний простору . Відомо також, що норма елемента дорівнює нормі відпо­відного йому елемента 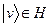, тобто

Але 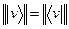. Отже, між множиною векторів типу 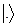і множиною векторів типу 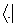є взаємно-однозначна відповідність.

Надалі вектор, який задається символом 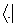услід за Діраком називатиме­мо бра-вектором (лівий), а вектор, який задається символом 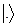– кет-векто­ром (правий). Символ зображає скалярний добуток бра-вектора на кет-вектор.

Як бачимо, у квантовій механіці так позначені вектори Ґільбертового просто­ру, що не існує скалярного добутку бра-вектора на бра-вектор, або кет-вектора на кет-вектор, а існує тільки скалярний добуток бра-вектора на кет-вектор.

Дата добавления: 2015-06-04