Лінійні оператори у просторі Ґільберта

Поняття оператора у функціональному Ґільбертовому просторі 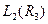. Оператором 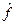, областю визначення якого є 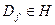, назвимо той рецепт, за яким функ­ції 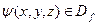ставимо у відповідність функцію

Це твердження зображають у вигляді

, , .

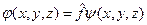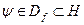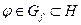У квантовій механіці використовують лінійні оператори. Це означає, що такі оператори задовольняють умову

тут , 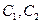– комплексні числа.

Сума та добуток операторів. Це оператори, які задовольняють умови

для будь-якої ,

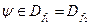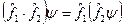для будь якої , .

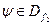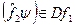Добре відомо (і ми побачимо це на прикладі), що частіше 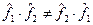. Якщо 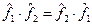, то кажуть, що оператори 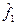і 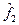комутують.

Природньо обґрунтовується поняття лінійного оператора і в абстрактному Ґільбертовому просторі :

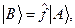
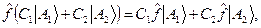
для любого ,

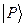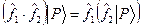для любого .

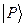Згадаємо, що для скалярного добутку трьохмірних векторів 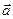і 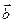часто вжи­вають символ 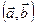. Це позначення можна «узагальнити» і на випадок векторів з 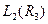. Записуватимемо скалярний добуток двох векторів 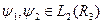у вигляді

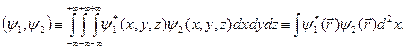
Тут ; ; .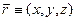

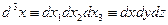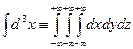Символом 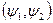скалярного добутку двох векторів зручно користувати­ся під час запровадження поняття спряженого оператора.

Спряжений оператор. Кожний лінійний оператор 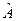в Ґільбертовому просторі має спряжений оператор, який позначається 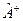та який визначається рівністю

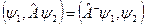для всіх ,

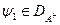При цьому

, , ;

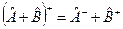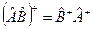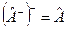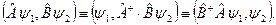
Ермітовий оператор. Лінійний оператор 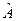в Ґільбертовому просторі нази­вається ермітовим (самоспряженим), якщо 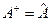, тобто має місце рівність

, для будь-яких .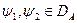

В інтегральній формі це означення виглядає так:

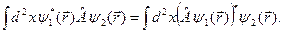
Важливий факт: якщо 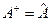, тоді

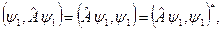
тобто скалярний добуток 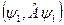для ермітового оператора є дійсною величиною.

Приклад 1. Задано оператори , , 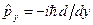, 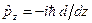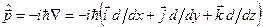. Легко довести, що , , 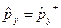, 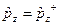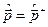. Доведемо це тільки для оператора 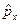. Для інших випадків доведення аналогічні.

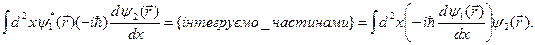
Припускається, що внесок 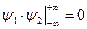. Надалі запровадимо позначення , , .

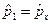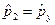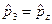Приклад 2. Оператори 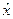, , 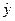, 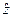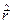множення на незалежну змінну:

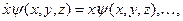
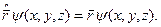
Задача. Доведіть, що мають місце такі операторні співвідношення:

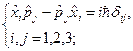
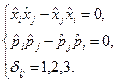
Щоб довести, наприклад, що має місце перше співвідношення, досить згадати таке очевидне співвідношення

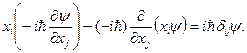
Приклад 3. Оператори народження та знищення. Ці оператори задають­ся рівностями

, .

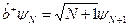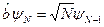Тут 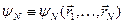– хвильова функція (тотожніх частинок) – «вектор» Ґіль­бертового простору.

Задача. Доведіть, що 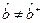, а оператор 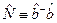є ермітовим.

Комутатор двох операторів 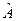і 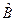. За означенням це оператор, який позначають як 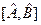, він такий:

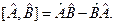
Отже,

, , .

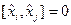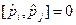Обернений оператор 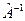до оператора 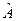. За означенням 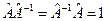. Якщо 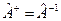, то такий оператор називають унітарним.

Власний вектор (функція) та власне значення лінійного оператора 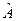у 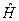– це такий вектор 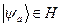, що

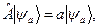
де 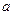– деяке число, яке називається власним значенням оператора 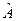. Якщо йдеться про власні функції 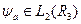, тоді останню рівність записуватимемо у вигляді:

.

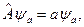
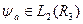У загальному випадку це рівняння має розв’язок не для довільних значень 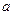, а тільки для певних 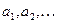Сукупність 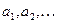може утворювати як дискретний ряд значень, так і неперервний у деякому інтервалі. Отже, величини 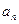, , це власні значення оператора 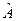, а відповідні їм функції (вектори) 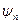– це власні функції оператора 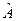. Сукупність власних значень оператора 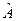нази­вають спектром цього оператора. Таким чином, рівняння на власні зна­чення (і власні функції) можна записати у вигляді

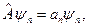
Зауваження. Якщо аргументами функції 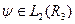є не декартові коорди­нати 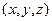, а, наприклад, сферичні 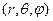, то для знаходження відповідних ди­ференціальних операторів необхідно зробити заміну змінних

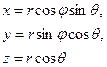
і користуючись загальними правилами, перейти від 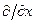, , 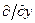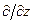до , , .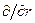

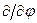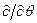Приклад 1. Оператор проекції моменту кількості руху .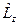

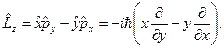
У сферичних координатах маємо:

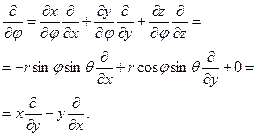
Отже, .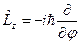

Задача. Знайти власні значення і власні функції оператора .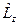

Розв’язання. Рівняння на власні функції і власні значення

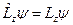
у сферичних координатах має вигляд:

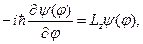
де азимутальний кут . Функція 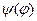, що задовольняє це рівняння, має вигляд

.

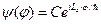Власні значення 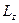знайдемо з умови однозначності хвильової функції :

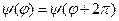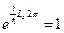, або , .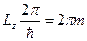

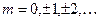Отже, як прийнято говорити у квантовій фізиці, власні значення проекції моменту кількості руху квантуються:

,

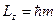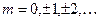
Сталу нормування 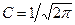знаходимо з умови нормування

.

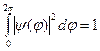Остаточно, власні функції оператора 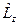запишемо так:

,

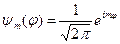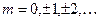
Властивості власних функцій та власних значень ермітових (самоспряже­них) операторів. Нехай 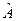– самоспряжений оператор, 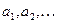– його власні зна­чення, а 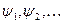– відповідні власні функції цього оператора.

Твердження 1. Власні значення самоспряженого оператора є дійсними.

Доведення. Умова самоспряженості дає

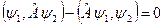, для будь-яких .

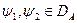Звідси для 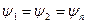маємо

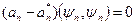, або .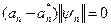

Тут ми скористаємося тим, що 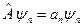. Оскільки , то .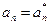

Твердження 2. Власні функції самоспряженого оператора утворюють ортонормовану систему функцій, якщо 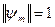, 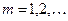. Це означає

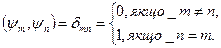
Доведення (для випадку дискретного спектра оператора 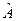; при умові, що 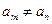, якщо 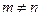). Умова самоспряженості дає

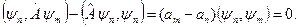
Якщо 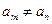, тоді 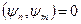. Якщо 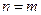, тоді за умовою теореми .

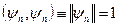Зауваження. Буває так званий вироджений дискретний спектр, коли одному власному значенню оператора 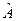відповідає декілька власних функцій. В цьому випадку можна здійснити так звану процедуру ортогоналіза­ції множини власних функцій. Про це іншим разом.

*⁾ Координатне зображення ще має назву x -зображення. У x -зображенні оператор – діагональний.

*⁾ Імпульсне зображення ще має назву p -зображенням. У p -зображенні оператор 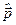– діагональний.

*⁾ Назва „замкнена” (повна) система функцій походить від того, що до сукупності 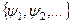вже не можна додати ще одну функцію, яка була б ортогональна до всіх функцій ψ_n, n =1,2,…

*⁾ Носій функції 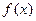– це множина (область) значень аргумента 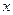, для яких функція відмінна від нуля. Позначають носій символом .

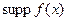*⁾ Питання про правомірність застосування рівняння К-Г-Ф до руху електрона ми тут не обговорюємо.

*⁾ Див. додаток до лекції.

Дата добавления: 2015-06-04