Власний магнітний момент електрона

Нерелятивістський перехід у рівнянні Дірака.Рівняння Паулі.

З самого початку ми обговоримо в цьому пункті лекції питання про те, коли має зміст квантова механіка однієї частинки. Відомо, що при енергіях 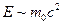, як показує дослід, має місце явище взаємоперетворення та народжен­ня нових частинок. Зокрема інтенсивність випромінювання та погли­нання світла 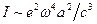, де . Виходить, що квантова механіка о днієї частинки має зміст лише за умови, якщо розглядаються процеси з енергіями . Це означає, що навіть точні рівняння ми повинні розкладати за степе­нями 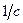, переходити до квазірелятивістського наближення цих рівнянь, обме­жуючись лише членами , а потім шукати розв’язки цих (вже наближених) рів­нянь. Якщо ми виходимо за межі наближення , то змушені враховувати про­цеси поглинання і випромінювання фотонів. Через це нас цікавитиме нереля­тивістський перехід у рівнянні Дірака для електрона із зарядом в електромаг­нітному полі з потенціалами та :

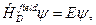
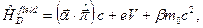
Нехай

, ,

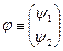Якщо тепер записати стаціонарне рівняння Дірака з Ґамільтоніаном 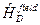через двомірні матриці Паулі, а потім використати прості та очевидні маніпуляції з цим рівнянням, то ми приведемо його до системи таких двох матричних рів­нянь відносно функцій 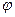і :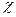

З другого рівняння одержуємо

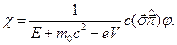
Тепер підставимо цей вираз для функції 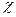у перше рівняння та знайдемо рівняння для :

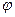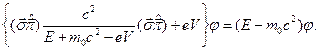
Будемо цікавитися рухом частинки (електрона) з додатною енергією (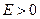). У цьому випадку при переході до нерелятивістської теорії, як ми вже знаємо, основну роль відіграє функція 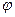(а 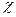є малою)*⁾. У рівнянні для 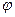енергію 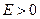відраховують від енергії спокою 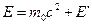та записують його у вигляді

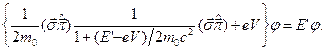
Тепер ми взмозі перейти у цьому рівнянні до нерелятивістської границі, коли член

Коли ми у знаменнику першого доданка лівої частини рівняння для 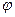знех­туємо членом , то одержимо шукане квазірелятивістське набли­ження з точністю до :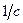

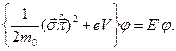
Запишемо добре відому з математики просту формулу, у справедливості якої легко переконатися самостійно:

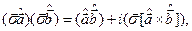
де 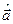і – довільні оператори. У нашому випадку , а тому ми маємо справу з квадра­том оператора 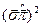, що входить у знайдене рівняння для .

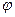Твердження.

де 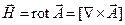– напруженість магнітного поля.

Доведення.

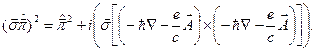
Розглянемо окремо вираз

Отже,

Таким чином, ми одержуємо так зване рівняння Паулі

Запровадимо у розгляд оператор

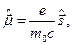
де, як нам відомо, оператор спіну . Тоді третій доданок у рівнянні Паулі ма­ти­ме вигляд 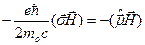і буде грати роль оператора енергії взаємодії власного магнітного моменту електрона 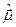із зовнішнім магнітним полем .

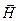Як бачимо, з теорії Дірака випливає не тільки наявність власного механіч­ного моменту частинки (спіна електрона), а й власного магнітного моменту. Стаціонарне рівняння Шредінґера для електрона у зовнішньому електромагніт­ному полі з потенціалами і виглядало

,

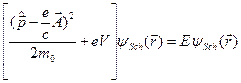отже, у ньому не враховувалась енергія взаємодії 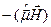. Рівняння Дірака враховує цю енергію і з великою точністю описує поведінку електронів.

Дата добавления: 2015-06-04